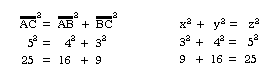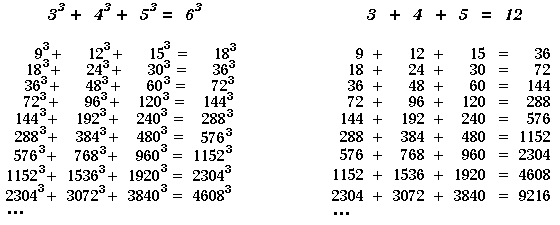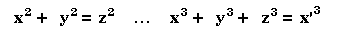
|
The Pythagorean Theorem and The Maya Long Count
The research on Science in Ancient
Artwork has led me to consider the Pythagorean Theorem in the
light of the positional level numbers/fractals of the maya
long count. Various essays deal with the possible extension
of the Pythagorean Theorem to the third power (to the cube)
in relation to the mathematical and geometrical appearance of
the maya long count fractals within progressive series
of right triangles.
It would appear that the 3-4-5 right triangle, and its multiples
and variations, may have served as a basis for the ancient reckoning
system of Mesoamerica. Extending the Pythagorean Theorem to
the cube produces the exact series of multiples within the maya
long count, something difficult to attribute to chance.
With the extension of the Pythagorean Theorem, not only is one
able to achieve a translation between right triangles on a series
of progression, but this is achieved through the maya
long count numbers/fractals.
Enclosed for your review is an extract, "The Extension of the
Pythagorean Theorem and the Maya Long Count". I would appreciate
receiving your comments or critical observations. Thank you.
Charles William Johnson
johnson@earthmatrix.com
Earth/matriX
The Extension of the Pythagorean
Theorem
and the Maya Long Count
Charles William Johnson
Various ancient cultures based
some of their artwork on the 3-4-5 right triangle, frequently
referred to by geometrists as a perfect triangle. Pythagoras
is cited as having understood the manner in which the three
sides of a right triangle are related. This proposition has
become known as the Pythagorean Theorem: the square of the hypotenuse
of a right triangle equals the sum of the squares of the legs.
This theorem may be expressed in different algebraic forms:
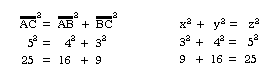
The first algebraic expression
relates to the lines of geometry; the second to the mathematical
one.
In our studies about Science in Ancient Artwork, we considered
extending the Pythagorean Theorem to the power of three. The
relation of equivalency among the terms of the equation vanish
due to geometric progression. Yet, in the light of the positional
level numbers/fractals of the maya long count system, it became
obvious created a distinct relation of equivalency:

This expression reveals the relationship
between right triangles adjacent to one another on a progression
of multiples of the 3-4-5 numbers:
PROP.- In a progression of 3-4-5 right triangles, the
cube of the shorter leg equals the sum of the cubes of the three
sides of the right triangle inmediately preceding it on the
progression.
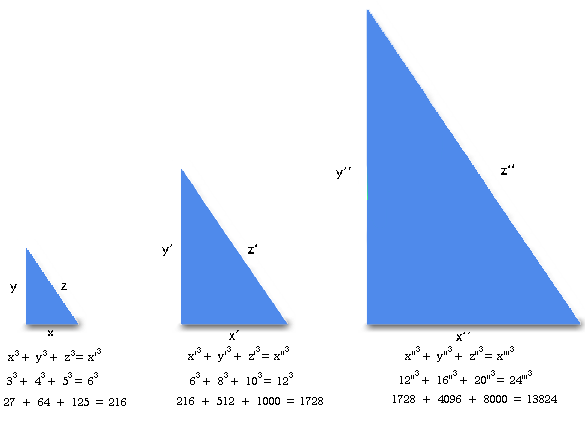
By applying the ancient mediatio/duplatio
method to the integers, the doubling/halving of the numbers
in the equation produces a progression that reflects the numbers/fractals
of the maya long count: 18, 36, 72, 144, 288, 576, 1152, 2304,
etc. Multiples occur even two or three times within a single
expression of the equation (in a right triangle's measurements).
They occur in relation to the multiples of the constant number's
progression; 1, 2, 4, 16, 32, 64, 128, etc. These two progressions
form the basis of the numbers/fractals of the maya long
count system as cited in the historical record.
The Extension of the Pythagorean Theorem:
The Positional Level Numbers/Fractals of the Maya Long Count
on the 3-4-5 Right Triangls Progression
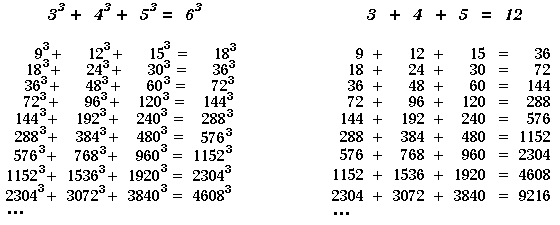
By knowing one number on the progression
cited, one may resolve all other unknowns to infinity on the
progression in either direction simply by doubling/halving the
integers in relation to the 3-4-5-6 relation. It could be stated
that by knowing one maya numbers/fractal, all maya
numbers/fractals may be known. The positional level numbers/fractals
of the maya long count reflect a knowledge of the Pythagorean
Theorem, as well as a knowledge of the possible extension of
the Pythagoren Theorem to the power of three. Other powers may
be easily involved in the computations as one derives distinct
relationships on the progression of numbers.
Ancient monuments around the world, also in Egypt and China,
appear to have been based on the 3-4-5 right triangle as of
the telltale numbers/fractals found in this particular progression
of values as explained by the extension of the Pythagorean Theorem
to the power of three.
Charles William Johnson
e-mail: johnson@earthmatrix.com
©1995-2013 Copyrighted by Charles William Johnson. All
Rights Reserved.
Reproduction prohibited without express written permission
from the author.
Earth/matriX
johnson@earthmatrix.com
For a more detailed analysis of
the extension of the Pythagorean Theorem, the maya long
count numbers/fractals, and their relationship to such questions
as Fermat's Last Theorem, consult the Earth/matriX books
"Science in Ancient Artwork and Science Today".
The Maya Long Count: an Extension of the Pythagorean
Theorem
and an Emendation to Fermat's Last Theorem
The Pythagorean Theorem
and The Maya Long Count
Summation of Fermat’s
Last Theorem (xn + yn = xn)
Fermat’s
Last Theorem: A Brief Summation
Fermat’s
Last Theorem: Powers and Last-Digit Patterns, (Relations
of Non-Equivalency and Approximate Equivalency)
Fermat’s
Last Theorem
|