Science in Ancient Artwork
and
Science Today
Fermat’s Last Theorem:
Powers and Last-Digit Patterns
(Relations of Non-Equivalency and Approximate Equivalency)
By Charles William Johnson
Recently, mathematicians have attempted to prove Fermat’s Last Theorem in an indirect manner. If the idea (Frey, 1985) that the elliptic curve Ea,b,c cannot exist because of its properties, then if proven correct, that no a, b, c, n may exist, it can be concluded that Fermat’s last theorem is true. In order to read this indirect proof, which does not direct Fermat’s last conjecture head on, one must sift through over a hundred pages of contemporary mathematical writing expressed mainly in alphabetical letters. In other words, the proposed proof does not really explain Fermat’s theorem in numbers, but in alphanumeric symbols.
What has been conclusively lacking for the past few hundred years is an acceptably brief explanation that might illustrate why Fermat’s last theorem may be correct, there are no answers or relations of equivalency to the equation,
xn + yn = zn
with the terms in whole numbers and with exponents/powers above two. Fermat wrote his last theorem on the margin of a book, musing that there was insufficient space to write the proof down. Had he thought the proof to consist of over one hundred pages of analysis, undoubtedly his humor would not have made any sense. A more extensive comment may have been in order. However, if we analyze the idea of his last theorem from the perspective of numbers and their behavior, we may come to realize why he proposed such a humorous thought. Any critique of contemporary proofs of Fermat’s Last Theorem becomes equally superfluous when we realize how easy we come to understand the workings of the proposed equation. More extensive analyses may be read in the Earth/matriX series of essays and extracts; for now, let us simply present how to conceive of Fermat’s Last Theorem from the perspective of powers and the last digits of the terms of the equation.
We begin this brief analysis by simply listing the natural numbers from one to infinity.
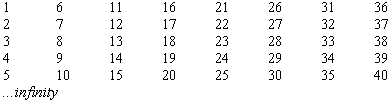 |
 |
The next step is to relate the powers (exponents of n) to
the natural numbers, again from one to infinity.
 |
By listing the natural numbers and their corresponding powers, one is able to distinguish a definite pattern that evolves for this particular relationship of the numbers. By listing the numbers in this manner, one may observe a definite pattern appear as of the last-digit numbers for each of the figures expressed on the previous table. In fact, these four patterns repeat themselves infinitely so, as we extend the natural numbers down towards infinity. Specific powers produce specific number endings. The four basic patterns of the series of numbers according to the powers are:
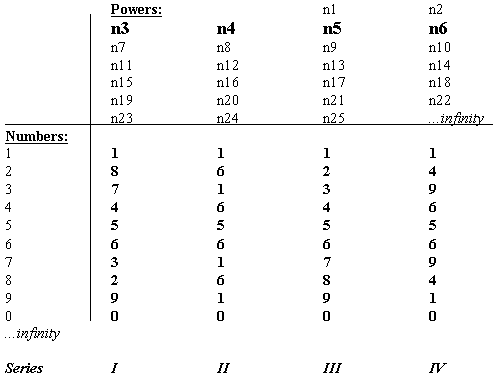
The previous table illustrates the four basic patterns of last digits produced as of the relationship between the natural numbers from one to infinity and their corresponding powers from one to infinity. These four basic patterns create four basic series of numbers that repeat themselves to infinity. In order to comprehend the meaning of these basic patterns for Fermat’s Last Theorem, we need limit our considerations to the powers n3, n4, n5, n6, given the fact that the conditions for the equation establish n as being above two. Needless to remark, it is significant that the powers that are relevant for explaining Fermat’s Last Theorem concern the numbers (3,4,5,6) as those which are relevant to the Pythagorean Theorem (3,4,5) and the extension of the Pythagorean Theorem (3,4,5,6) as we have analyzed else where (Cfr., Earth/matriX, Essay No.57).
Now, in order to develop relations of equivalency among the terms (x,y,z,n) of the cited equation, one would necessarily have to find any two natural numbers on any one of the four series whose sum would constitute an equivalency to a third number on that same series, for the same power (n). As Fermat posed off-handedly, such a relationship of equivalency does not exist in whole numbers. In fact, the relationship does not exist at all, given that any relation of apparent equivalency with decimally fractional numbers for z simply represents an approximation of equivalency of values.
Furthermore, in order to explain and grasp the nature of the patterns of equivalency (non-equivalency), one need only analyze the four basic patterns, given the fact that said patterns shall be repeated as one travels up the scale of values to relationships of higher numbers. Mathematicians have proven the impossibility of the equation most recently up to over 4,000,000 powers (Buhler, et.al., 1993), when in fact analyses could have ended over a century ago, when Kummer (1847) finished the analyses already achieved by Euler who analyzed n3 (1753), and Legendre (1825) analyzed n5. Kummer need only have analyzed n6, since Fermat himself had already analyzed n4 (ca. 1640). In other words, to prove Fermat’s Last Theorem, one need only analyze and prove the four basic patterns for the natural numbers up to the number twenty, at the most, and for the four powers, n3, n4, n5, n6, given the fact that the patterns repeat themselves for all other numbers to infinity. All efforts after 1847 have simply been a certain inability to explain to ourselves the nature and behavior of the cited equation, i.e., why and how it performs as it does.
In order to illustrate our point, we need simply offer a few examples based on the implied rule of addition within the stated equation. In a certain sense, the algebraic expression of Fermat’s Last Theorem may be the reason for not comprehending the inner workings of the numbers implied. The symbolic representation of numbers has led to great things in contemporary history. Yet, the symbolic representation of numbers somehow draws one ever further away from the numbers themselves. Let us consider the equation at the level of the performance of the numbers and their products, instead of at the level of the symbolic representation (x,y,z,n) of the terms of the equation.
In order for a possible relation of equivalency to exist, according to the simple rules of addition within mathematics, the last digits of the products of the first two terms (x, y) must add up to the corresponding last digit of the product of the third term (z) of the equation. In other words, if the last digit of the first term is 1, and the last digit of the second term is a 2, then the last digit of the third term must necessarily be a three, and so on. In order to comprehend the nature of the equation expressed in Fermat’s Last Theorem, we need only comprehend this simple rule and observe its performance on the four basic patterns. Let us offer a few examples, since after a brief analysis of the four basic patterns, one realizes the futility of seeking such a relationship of equivalency.
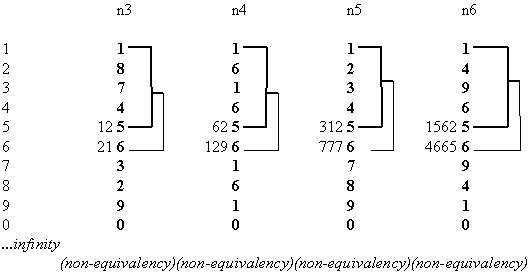
No matter which two particular numbers are chosen for x and y, the next whole number on the series whose last digit corresponds to the required sum for the last digits of those first two terms, shall always represent a product that is greater than the sum required for the sum of the first two products of x and y. One may state the obvious inversely: for any chosen number/product of the term z, the two lesser products whose last digits may add up to the last digit of the third product shall always represent the sum of two products less than the third product. Given the fact that Fermat’s Last Theorem is strapped to this simple rule of addition, no two numbers/products on the infinite series of natural numbers and their basic powers (also to infinity) may offer a solution. This simple rule of addition applies to all natural numbers (products) and to all powers of those numbers (products).
One need only view what the supposed relations of equivalency would look like for the previous examples, in order to understand the inner workings of the cited equation.
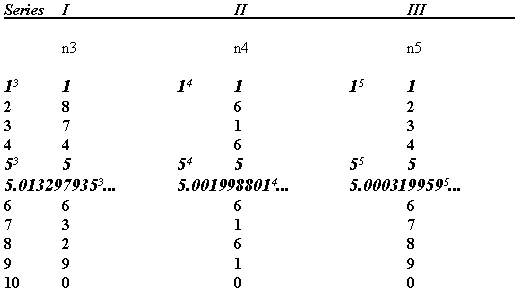 |
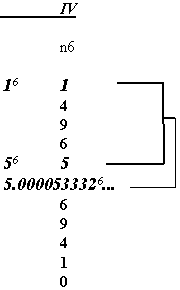 |
The previous examples of the terms 1 plus 5 to the power of 3, 4, 5, or 6 reveal a third term which is a fractional expression to the respective power. These relations are in themselves only approximate equivalencies given the unending fractions. In fact, regarding the particular equation cited in Fermat’s Last Theorem there are no relations of equivalency either in whole numbers or in fractional numbers. No relations of equivalency exist for the equation at all. In order to observe more extensive examples, consult some of the Earth/matriX essays regarding this particular equation.
At the level of terms (xn, yn) one may choose any two numbers in order to possibly find a third term (z). However, at the level of the products of these terms, one may only choose two products/numbers whose last digits correspond in addition to the last digit of the third product/number. Within the series I and III, all natural numbers may be chosen for effecting possible computations in a search for relations of equivalency, given the fact that all natural numbers appear within the last digits of the patterns. Within the series IV those natural numbers whose products yield a last digit of 2, 3, 7, and 8 are eliminated from such possibilities. And, within series II, those natural numbers whose products yield a last digit of 2, 3, 4, 7 and 9 are eliminated from such possibilities. For these numbers of series II and IV do not appear within the corresponding patterns of last digits.
From the previous analysis, one may understand that Pierre de Fermat was correct in surmising that the cited equation has no solutions in whole numbers. But, not only that, there are no solutions of equivalency for any numbers, given the fact that even those apparent relationships of equivalency expressed in fractional numbers for the term z, are mere approximations. Furthermore, this may be held true for all the natural numbers from one to infinity and, for all of the possible powers expressed in whole natural numbers from one to infinity. One need only analyze for the proof the first ten or twenty natural numbers in order to extrapolate for the remaining infinite number of natural numbers. And, one need only analyze the natural numbers in relation to the four initial powers/exponents of n3, n4, n5, and n6 in order to extrapolate for all of the infinite powers/exponents remaining. For the pattern given in n4, for example, is the same for its multiple, n40000000, as shown in the table above. Our analysis does not deny the significance of the analyses based on considerations for elliptic curves. That particular subject would require another essay. However, one may conclude from our analysis, that a more economical explanation of Fermat’s Last Theorem is readily accessible in terms of the natural numbers and the laws of simple addition.
*********
johnson@earthmatrix.com
Fermat's Last Theorem:
A Brief Summation
Summation
of Fermat's Last Theorem
Fermat's
Last Theorem
Science in Ancient Artwork and Science Today Series
Fermat’s Last Theorem: Powers and Last-Digit Patterns
Extract No.38.
2 November 1998.
©1998-2012 Copyrighted by Charles William Johnson. All Rights Reserved.
Reproduction Prohibited.
| Home | Books | Author |