Science in Ancient Artwork
Fermat's Last Theorem
By
Charles William Johnson
36 |
: |
64 |
: |
100 |
48 |
: |
52 |
: |
100 |
Science in Ancient Artwork Series
Fermat's Last Theorem
Pierre the Fermat's Last Theorem is a conjecture about the impossibility of the equation
| (1) |
when the terms (x ,y ,z ,n) are whole numbers with n greater than 2. In order to understand how the numbers behave, the equation must be considered where the terms may be fractions and/or whole numbers and n may be any number. Aside from x + y = z, the initial equation begins then with
| x2 + y2 = z2 | (2) |
which represents the Pythagorean Theorem, reflecting the relation of equivalency among the sides of right triangles. Equivalency may be expressed in fractions/whole numbers combined (right triangles), or in whole numbers alone (perfect right triangles).
Whenever fractions are involved, the relation of equivalency always represents an approximation. Nonetheless, mathematicians and geometrists accept that numerical expression as being equivalent. Perfect right triangles represent exact equivalencies expressed in whole numbers. The 3-4-5 perfect right triangle, and its series of multiples (6-8-10...), alongwith its series of variations (5-12-13...) are determinant for understanding Fermat's Last Theorem. Irrespective of the power involved, the addition of the terms x and y must share complementary percentiles of the lue z (100%).
| 32 + 42 | = | 52 | 62 + 82 | = | 102 | |
| 9 + 16 | = | 25 | 36 + 64 | = | 100 | |
| 25 | = | 25 | 100 | = | 100 |
-
furthermore,
 |
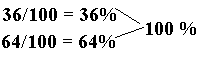 |
All multiples of the 3-4-5 perfect right triangle reflect this 36:64:100 percentile relationship.
An alternative expression of the Pythagorean Theorem for the variation of the 3-4-5 perfect right triangle involves
| x2 | = | y + z | (3) |
| 52 | = | 12 + 13 | |
| 25 | = | 25 |
-
furthermore,
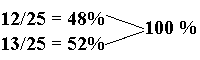 |
Applying the original equation (2) of the Pythagorean Theorem to this particular variation of the perfect right triangle would produce a distinct percentile relationship (.14792899408:.85207100591) from the 48:52:100 relation.
The 3-4-5 perfect right triangle series (including multiples and variations) is the only expression of the equation where all of the terms within the equation itself are whole numbers: the roots (3-4-5); the products of those roots (9-12-25) and; the percentile numbers (36:64:100). This same combination of numbers in whole number terms would have to occur at powers greater than 2 in order to obtain relation of equivalency that would involve whole numbers only. The appearance of a fractional number in any one of the numbers would impede such an appearance.
At higher powers, this particular relation of equivalency produced by the 3-4-5 perfect right triangle disappears: for example,
| 63 + 83 | 103 | 6 | 10 |
||||
| 216 + 512 | 1000 | 1296 + 4096 | 1000 | ||||
| 728 | 1000 | 5392 | 1000 |
The relation of equivalency in 62 + 82 = 102 breaks down due to geometric progression. However, one may than consider applying the Pythagorean Theorem in another manner; consider the following arrangement:
| 63 | + | 83 | = | z |
6 |
+ | 8 |
= | z |
|
| 216 | + | 512 | = | z |
1296 | + | 4096 | = | z |
|
| 728 | = | z |
5392 | = | z |
-
further,
-
then,
| 6 3 + 8 3 | = | 8.9958828913 | 6 |
= | 8.56914459 |
Within the Pythagorean Theorem, these higher power relations represent acceptable examples of equivalency even though they are expressed in fractions.
By adding zeros to the above numbers, the decimal place is removed and whole numbers appear on the calculator:
| 60000000003 | + | 80000000003 | = | 89958828903 |
| 6000000000 |
+ | 8000000000 |
= | 8569144590 |
however, that is not the case since, for example, the calculator rounded off to 8569144590 which is actually 85691445899... as a root. Nonetheless, for computational needs, this relations of equivalency is perfectly acceptable, just as any fractional expression of the Pythagorean Theorem is considered to be equivalent. Fractional expressions constitute acceptable relations of equivalency for any power.
In general, then, the equation x![]() + y
+ y![]() = z
= z![]() represent relations of equivalency in fractions alone, fractions with
whole numbers, or whole numbers alone. However, the relations of equivalency
expressed in whole numbers alone occur only at the power of 2 for measurements
of multiples and variations of the 3-4-5 perfect right triangle. All other
combinations of fractions or fractions and whole numbers together occur
at any power.
represent relations of equivalency in fractions alone, fractions with
whole numbers, or whole numbers alone. However, the relations of equivalency
expressed in whole numbers alone occur only at the power of 2 for measurements
of multiples and variations of the 3-4-5 perfect right triangle. All other
combinations of fractions or fractions and whole numbers together occur
at any power.
The particular conditions imposed by Fermat, that this equation represent only whole numbers for powers greater than 2 deny the possibility of achieving a relation of equivalency given the procedure of the addition of two of the terms. The hidden numbers of the percentiles must also be whole numbers in relationship to the whole numbers of the terms (x, y, x, n) and their products. Consider the percentile numbers of the previous example which appeared to represent whole numbers on the calculator:
| 216/728 | = | .2967032967 ... | 1296/5392 | = | .24035608308 ... | |
| 512/728 | = | .70329670329 ... | 4096/5392 | = | .75964391691 ... | |
| + |
|
+ |
|
|||
| .99999999999 ... | .99999999999 ... |
No two whole numbers, above the square, after undergoing the multiplication process known as powers of itself, will produce two numbers whose products will add up to 100% the value of a third whole number's product to that same power. Such a relation of equivalency only occurs for the series of perfect right triangles represented by the measurements 3-4-5 and their multiples (6-8-10 ...) and variations (5-12-13 ...). One may even visualize how the 3-4-5 numbers of the perfect right triangle, and their multiples and variations, represent a cut-off point on a table of roots and powers.
| x |
x |
x |
x |
x |
x |
||||||||||||||
| root/product | root/product | root/product | root/product | root/product | |||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 2 | 4 | 2 | 8 | 2 | 16 | 2 | 32 | 2 | 64 | ||||||||||
| 3 | 9 | 3 | 27 | 3 | 81 | 3 | 243 | 3 | 729 | ||||||||||
| 4 | 16 | 4 | 64 | 4 | 256 | 4 | 1024 | 4 | 4096 | ||||||||||
| 5 | 25 | 5 | 125 | 5 | 625 | 5 | 3125 | 5 | 15625 | ||||||||||
| 6 | 36 | 6 | 216 | 6 | 1296 | 6 | 7776 | 6 | 46656 | ||||||||||
| 7 | 49 | 7 | 343 | 7 | 2401 | 7 | 16807 | 7 | 117649 | ||||||||||
| 8 | 64 | 8 | 512 | 8 | 4096 | 8 | 32768 | 8 | 262144 | ||||||||||
| 9 | 81 | 9 | 729 | 9 | 6561 | 9 | 59049 | 9 | 531441 | ||||||||||
| 10 | 100 | 10 | 1000 | 10 | 10000 | 10 | 100000 | 10 | 1000000 | ||||||||||
| 11 | 121 | 11 | 1331 | 11 | 14641 | 11 | 161051 | 11 | 1771561 | ||||||||||
| 12 | 144 | 12 | 1728 | 12 | 20736 | 12 | 248832 | 12 | 2985984 | ||||||||||
| 13 | 169 | 13 | 2197 | 13 | 28561 | 13 | 371293 | 13 | 4826809 | ||||||||||
| 14 | 196 | 14 | 2744 | 14 | 38416 | 14 | 537824 | 14 | 7529536 | ||||||||||
| 15 | 225 | 15 | 3375 | 15 | 50625 | 15 | 759375 | 15 | 11390625 | ||||||||||
| 16 | 256 | 16 | 4096 | 16 | 65536 | 16 | 1048576 | 16 | 16777216 | ||||||||||
| 17 | 289 | 17 | 4913 | 17 | 83521 | 17 | 1419857 | 17 | 24137569 | ||||||||||
| 18 | 324 | 18 | 5832 | 18 | 104976 | 18 | 1889568 | 18 | 34012224 | ||||||||||
| 19 | 361 | 19 | 6959 | 19 | 130321 | 19 | 2476099 | 19 | 47045881 | ||||||||||
| 20 | 400 | 20 | 8000 | 20 | 160000 | 20 | 3200000 | 20 | 64000000 | ||||||||||
| ... | ... | ... | ... | ... | |||||||||||||||
Due to the geometric progression that sets in, no other combination of roots and powers greater than 2, reproduce the distinguishable 100% relation of the addition of terms and equivalency together, for all of the terms involved: roots:products:percentiles in whole numbers. And, because numbers behave in this manner for perfect right triangles, different ancient cultures may have chosen the 3-4-5 right triangle for their artwork. The 3-4-5 perfect right triangle, alongwith its multiples and variations, not only distinguishes itself in equations to the power of two, but allows for understanding its absence in all powers greater than 2. This may also explain one of the reasons why ancient mathematicians and geometrists preferred whole numbers.
For more detailed analyses of the ideas treated in this extract:
Fermat's
Last Theorem: A Brief Summation
Fermat’s Last Theorem: Powers
and Last-Digit Patterns
Summation
of Fermat's Last Theorem
©1998-2012 Copyrighted by Charles William Johnson. All rights reserved.
Your comments and suggestions are greatly appreciated:
e-mail: johnson@earthmatrix.com
Science in Ancient Artwork
Fermat's Last Theorem
Extract No.2
©1998-2012 Copyrighted by Charles William Johnson. All Rights Reserved
Earth/matriX,
Reproduction prohibited without written consent of the author.
| Home | Books | Forum | Reviews | Author |