In the seventeenth century, Pierre de Fermat made a conjecture as to the impossibility of resolving the equation,
xⁿ + yⁿ = zⁿ, where the terms are whole numbers, and the exponent is greater than two.

Most attempts at proving Fermat's conjecture have been effected at the level of the equation's terms and their exponents. The intent has been to find those elusive and unique numbers that would produce a relation of equivalency. One recent attempt at a proof involved computations of exponents to £ 4000000. An attempt at an indirect proof has been offered as of the behavior of elliptic curves. Although not recognized as such, the proof of Fermat's conjecture was achieved centuries ago when the exponents of n3, n4, n5, and n6 were analyzed. And, in fact, the proof may be achieved as of these powers in relation to the first twenty natural numbers.

Terms and powers are shorthand notations for multiplication, whereby products are obtained in the computations. A direct proof to Fermat's Last Theorem concerns the analysis of the patterns of last-digit termination of the products; in this case, the products of the terms and exponents of the proposed equation. All whole-number exponents (1 to ¥) of all the natural numbers (1 to ¥) produce four distinct patterns of the last-digit terminations of their products. In the case at hand, the natural numbers (1 - ¥) multiplied to the powers (n3 to infinity) as shown, produce these repeat patterns of last-digit terminations in their products.

Therefore, the cited equation of xⁿ + yⁿ = zⁿ.ultimately resolves itself through the simple addition of terms: the product of xⁿ plus the product of yⁿ equals the product of zⁿ. The patterns of the last-digits determine the possibility or impossibility of equivalencies through addition. Since all natural numbers and powers thereof produce these patterns, one need only analyze the stipulated addition of the products for n3, n4, n5, n6. All computations resulting from the remaining exponents (n7 to infinity) will obey the same rule of possibility or impossibility of addition as do the powers n3, n4, n5, and n6. Therefore, one could analyze n7, n8, n9, n10, or n11, n12, n13, n14, etc., with the same conclusions for all other powers and numbers. Now, let us visualize a specific example of last-digit termination: ...1 + ...5 = ...6.

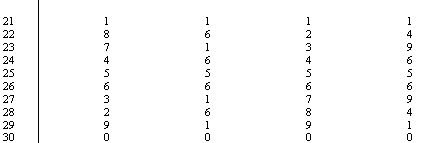
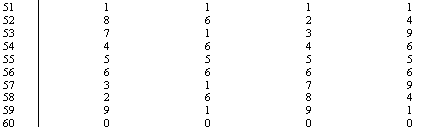Any two products (numbers) chosen to be added, must have their last-digits add up to and correspond to the last-digit termination of the third product (number). The repeat patterns of the last-digit terminations cause such an equivalency to become impossible. For no matter which two products on the series are chosen as in the example, the third product (z) according to simple addition, would necessarily have to end in a last-digit termination that results from the simple addition of the first two products (x, y). The next last-digit termination corresponding to any example always represents a product (number) of higher value than the sum of the first two products added together. When the last-digit termination does correspond in equivalency to the sum of the first two products, it always represents the product of a decimal number (term) to any power greater than two.

Fermat's Last Theorem represents an impossibility for attaining relations of equivalency for any number or any power greater than two, whether it be in whole numbers or in fractions. Any supposed relation of equivalency concerning both whole numbers and fractional expressions represents only an approximation. The relations of approximation are not relations of equivalency, but of approximate equivalency. Values are either equivalent or not equivalent; that is what the word "equivalent" means etymologically speaking. [The only equivalency of fractions, that may be considered, are possibly those related to the unending fractions produced by the reciprocal of seven .142857142857142857..., which would require a separate discussion.]

Although not recognized as such, the conjecture made by Pierre de Fermat, known as Fermat's Last Theorem, was proven long ago, when the powers n3, n4, n5, and n6 were computed. What holds for these powers, holds for all whole-number powers, given the repeat patterns of last-digit terminations of the products of the terms and exponents of the equation. Therefore, there is no need to further seek a proof of the cited equation beyond these powers. The indirect proofs offered to date do not constitute a proof of the theorem. A proof of Fermat's Last Theorem can only be explained as of the repeat patterns of the last-digit terminations of the products of the terms and exponents of the equation, with regard to the laws of simple addition. The alpha-symbolic representation of Fermat's Last Theorem has possibly contributed to its misapprehension, since it may have caused some scholars to concentrate their analytical efforts on the terms and exponents of the equation, instead of on the products of those terms and exponents. Our direct proof of Fermat's Last Theorem has been resolved and explained in terms of numbers and how these behave in simple addition and multiplication.

Charles William Johnson, email: johnson@earthmatrix.com

***

Earth/matriX:
Science in Ancient Artwork and Science Today Series
Extract 51
Fermat's Last Theorem: A Brief Summation.