and Science Today
The Maya Long Count:
an Extension of the Pythagorean Theorem
and an Emendation to Fermat's Last Theorem
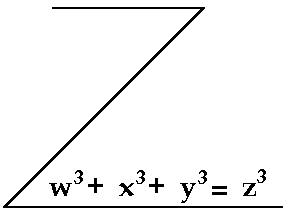
No.56
New Orleans, Louisiana.
|
|
|
The numbers related to the multiples of the 3-4-5 right triangle appear to reflect the number sets of the maya long count and the constant numbers of the 1,4,8,16,32,64,128,256, etc. progression. Furthermore, it would also appear that when the multiples of the 3-4-5 right triangle undergo relationships of equivalency to the power of three, there appears to exist a modification or extension of the Pythagorean Theorem. Also, these same computations would appear to suggest a different way of conceptualizing Fermat's Last Theorem. The fact that the numbers resulting from the charts devised by the author around the 3-4-5 right triangle seem to be directly related to the maya positional level numbers/fractals would suggest a possible manner of computation. The 3-4-5 right triangle may have served as the basis for devising and adopting the multiples of the maya long count numbers/fractal, as they both appear to enjoy the same kind of logic in the interplay of numbers; especially, the two number sets based on the 36c and the 64c numbers/fractals. The 36 x 64 combination produces the 2304 maya alautun number/fractal. Also, the addition of the two numbers equals 100 (36 + 64), which together form the twofold multiple of the 3-4-5 right triangle to the power of two: 6-8-10 to the power of two yields the 36-64-100 relation, which also serves as the logic of numbers of the maya long count. |
|
Table of Contents THE MAYA LONG COUNT:
|
by Charles William Johnson
Introduction
The 3-4-5 right triangle is extremely significant for understanding possibly the origin of the maya long count numbers/fractals: 18,36,72,144,288,576,1152,2304,4608,9216, etc. The numerical system is obviously based on the doubling/halving of the integers as we have been discussing and illustrating in the Earth/matriX series of essays. We have also seen how the maya long count numbers/fractals appear in many different unsuspecting environments, such as in the distance that the sun travels in a specific 20-day period of time (Earth/matriX No. 36). The also occur sporadically in minimax polynomials of the Fibonacci numbers (Horadam). We have also shown how they repeat themselves throughout the numbers related to the right triangle measurements and related powers.
Now, let us examine more closely alternative ways of conceptualizing the 3-4-5 right triangle; its different multiples and related powers of 2 and 3, the square and the cube of the 3-4-5 right triangle. The numbers that become evident from this mediatio/duplatio procedure would appear to suggest an extension of the Pythagorean theorem and a possible emendation to Fermat's conjecture or the last theorem.
Multiples of the 3-4-5 Right Triangle
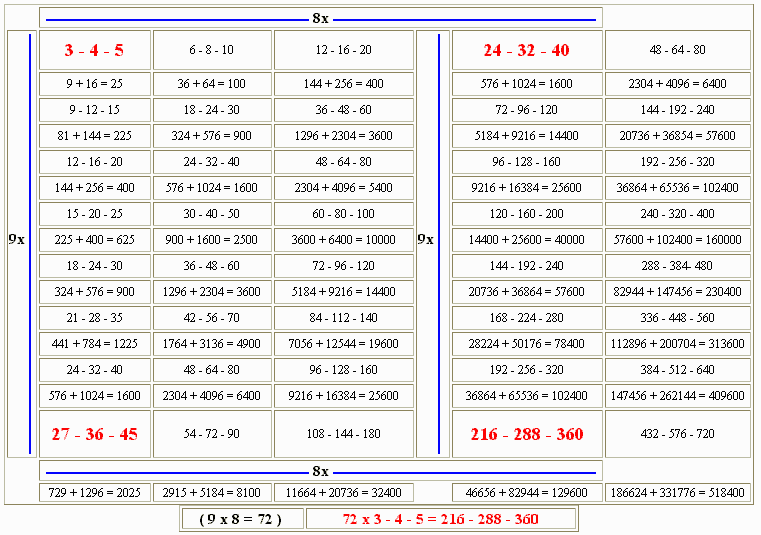
In the following chart we have simply offered multiples of the 3-4-5 right triangle in a series as indicated by the number of times multiplied in each column.
| 1x | 2x | 4x | 8x | 16x | ... | |
|---|---|---|---|---|---|---|
| 1x | 3 - 4 - 5 | 6 - 8 - 10 | 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 | ... |
| 9 + 16 = 25 | 36 + 64 = 100 | 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 6400 | ... | |
| 3x | 9 - 12 - 15 | 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 | ... |
| 81 + 144 = 225 | 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36854 = 57600 | ... | |
| 4x | 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 | ... |
| 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 5400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 | ... | |
| 5x | 15 - 20 - 25 | 30 - 40 - 50 | 60 - 80 - 100 | 120 - 160 - 200 | 240 - 320 - 400 | ... |
| 225 + 400 = 625 | 900 + 1600 = 2500 | 3600 + 6400 = 10000 | 14400 + 25600 = 40000 | 57600 + 102400 = 160000 | ... | |
| 6x | 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 | 288 - 384- 480 | ... |
| 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36864 = 57600 | 82944 + 147456 = 230400 | ... | |
| 7x | 21 - 28 - 35 | 42 - 56 - 70 | 84 - 112 - 140 | 168 - 224 - 280 | 336 - 448 - 560 | ... |
| 441 + 784 = 1225 | 1764 + 3136 = 4900 | 7056 + 12544 = 19600 | 28224 + 50176 = 78400 | 112896 + 200704 = 313600 | ... | |
| 8x | 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 | 384 - 512 - 640 | ... |
| 576 + 1024 = 1600 | 2304 + 4096 = 6400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 | 147456 + 262144 = 409600 | ... | |
| 9x | 27 - 36 - 45 | 54 - 72 - 90 | 18 - 144 - 180 | 216 - 288 - 360 | 432 - 576 - 720 | ... |
| 729 + 1296 = 2025 | 2915 + 5184 = 8100 | 11664 + 20736 = 32400 | 46656 + 82944 = 129600 | 186624 + 331776 = 518400 | ... | |
| ... | ... | ... | ... | ... | ... | ... |
The horizontal reading of the multiples regards the constant number series of 1, 2 , 4, 8, 16, 32, 64, 128, 256, 512..., which we have discussed earlier as an essential multiple series of the maya long count in relation to the positional level numbers/fractals of the maya long count itself: 9, 18, 36, 72, 144, 288, 576, 1152, 2304... The vertical reading of the previous chart reflects simply the 3-4-5 right triangle in a simple progression of unit multiples with an increment of one (1,2,3,4,5,6,7,8,9...). The different numerical combinations that derive from this procedure, as we shall examine herein, would seem to substantiate further the possibility that such a computational procedure may have been at the basis of the maya long count system, and the use of the 3-4-5 right triangle in maya artwork as some authors have also pointed out in their analyses (Harleston).
| 3 - 4 - 5 | 6 - 8 - 10 | 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 |
| 9 + 16 = 25 | 36 + 64 = 100 | 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 6400 |
| 9 - 12 - 15 | 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 |
| 81 + 144 = 225 | 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36854 = 57600 |
| 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 |
| 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 5400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 |
| 15 - 20 - 25 | 30 - 40 - 50 | 60 - 80 - 100 | 120 - 160 - 200 | 240 - 320 - 400 |
| 225 + 400 = 625 | 900 + 1600 = 2500 | 3600 + 6400 = 10000 | 14400 + 25600 = 40000 | 57600 + 102400 = 160000 |
| 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 | 288 - 384- 480 |
| 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36864 = 57600 | 82944 + 147456 = 230400 |
| 21 - 28 - 35 | 42 - 56 - 70 | 84 - 112 - 140 | 168 - 224 - 280 | 336 - 448 - 560 |
| 441 + 784 = 1225 | 1764 + 3136 = 4900 | 7056 + 12544 = 19600 | 28224 + 50176 = 78400 | 112896 + 200704 = 313600 |
| 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 | 384 - 512 - 640 |
| 576 + 1024 = 1600 | 2304 + 4096 = 6400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 | 147456 + 262144 = 409600 |
| 27 - 36 - 45 | 54 - 72 - 90 | 108 - 144 - 180 | 216 - 288 - 360 | 432 - 576 - 720 |
| 729 + 1296 = 2025 | 2915 + 5184 = 8100 | 11664 + 20736 = 32400 | 46656 + 82944 = 129600 | 186624 + 331776 = 518400 |
Once we have obtained different series of numbers for multiples of the 3-4-5 right triangle, it is then possible to apply the Pythagorean Theorem and obtain the squares of the different numbers.
| 3 - 4 - 5 | 6 - 8 - 10 | 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 |
| 9 + 16 = 25 | 36 + 64 = 100 | 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 6400 |
| 9 - 12 - 15 | 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 |
| 81 + 144 = 225 | 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36854 = 57600 |
| 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 |
| 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 5400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 |
| 15 - 20 - 25 | 30 - 40 - 50 | 60 - 80 - 100 | 120 - 160 - 200 | 240 - 320 - 400 |
| 225 + 400 = 625 | 900 + 1600 = 2500 | 3600 + 6400 = 10000 | 14400 + 25600 = 40000 | 57600 + 102400 = 160000 |
| 18 - 24 - 30 | 36 - 48 - 60 | 2 - 96 - 120 | 144 - 192 - 240 | 288 - 384- 480 |
| 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36864 = 57600 | 82944 + 147456 = 230400 |
| 21 - 28 - 35 | 42 - 56 - 70 | 84 - 112 - 140 | 168 - 224 - 280 | 336 - 448 - 560 |
| 441 + 784 = 1225 | 1764 + 3136 = 4900 | 7056 + 12544 = 19600 | 28224 + 50176 = 78400 | 112896 + 200704 = 313600 |
| 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 | 384 - 512 - 640 |
| 576 + 1024 = 1600 | 2304 + 4096 = 6400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 | 147456 + 262144 = 409600 |
| 27 - 36 - 45 | 54 - 72 - 90 | 108 - 144 - 180 | 216 - 288 - 360 | 432 - 576 - 720 |
| 729 + 1296 = 2025 | 2915 + 5184 = 8100 | 11664 + 20736 = 32400 | 46656 + 82944 = 129600 | 186624 + 331776 = 518400 |
From these two sets of numbers (the multiples of the 3-4-5 right triangle and their squares), the maya long count numbers/fractals become obvious in most cases as we have pointed out in the following chart. It is only with respect to the two series beginning with 81 and 324 that they are not obvious; but one only has to divide the integers of those series by the numbers 36 or those of the maya long count system itself (18,36,72,144, etc.) in order to see them make their appearance.
| 3 - 4 - 5 | 6 - 8 - 10 | 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 |
| 9 + 16 = 25 | 36 + 64 = 100 | 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 6400 |
| 9 - 12 - 15 | 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 |
| 81 + 144 = 225 | 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36854 = 57600 |
| 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 |
| 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 5400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 |
| 15 - 20 - 25 | 30 - 40 - 50 | 60 - 80 - 100 | 120 - 160 - 200 | 240 - 320 - 400 |
| 225 + 400 = 625 | 900 + 1600 = 2500 | 3600 + 6400 = 10000 | 14400 + 25600 = 40000 | 57600 + 102400 = 160000 |
| 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 | 288 - 384- 480 |
| 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36864 = 57600 | 82944 + 147456 = 230400 |
| 21 - 28 - 35 | 42 - 56 - 70 | 84 - 112 - 140 | 168 - 224 - 280 | 336 - 448 - 560 |
| 441 + 784 = 1225 | 1764 + 3136 = 4900 | 7056 + 12544 = 19600 | 28224 + 50176 = 78400 | 112896 + 200704 = 313600 |
| 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 | 384 - 512 - 640 |
| 576 + 1024 = 1600 | 2304 + 4096 = 6400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 | 147456 + 262144 = 409600 |
| 27 - 36 - 45 | 54 - 72 - 90 | 108 - 144 - 180 | 216 - 288 - 360 | 432 - 576 - 720 |
| 729 + 1296 = 2025 | 2915 + 5184 = 8100 | 11664 + 20736 = 32400 | 46656 + 82944 = 129600 | 186624 + 331776 = 518400 |
One should also note that the 441 and 729 series of numbers/fractals are also divisible by 36, but this does not produce the maya long count numbers/fractals. Possibly one of the most significant points is to note that the multiples derived from the multiplication of 7 (7x), do not reflect the maya long count fractals at any set of terms (either as multiples or as squares).
| 3 - 4 - 5 | 6 - 8 - 10 | 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 |
| 9 + 16 = 25 | 36 + 64 = 100 | 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 6400 |
| 9 - 12 - 15 | 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 |
| 81 + 144 = 225 | 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36854 = 57600 |
| 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 |
| 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 5400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 |
| 15 - 20 - 25 | 30 - 40 - 50 | 60 - 80 - 100 | 120 - 160 - 200 | 240 - 320 - 400 |
| 225 + 400 = 625 | 900 + 1600 = 2500 | 3600 + 6400 = 10000 | 14400 + 25600 = 40000 | 57600 + 102400 = 160000 |
| 18 - 24 - 30 | 36 - 48 - 60 | 2 - 96 - 120 | 144 - 192 - 240 | 288 - 384- 480 |
| 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36864 = 57600 | 82944 + 147456 = 230400 |
| 21 - 28 - 35 | 42 - 56 - 70 | 84 - 112 - 140 | 168 - 224 - 280 | 336 - 448 - 560 |
| 441 + 784 = 1225 | 1764 + 3136 = 4900 | 7056 + 12544 = 19600 | 28224 + 50176 = 78400 | 112896 + 200704 = 313600 |
| 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 | 384 - 512 - 640 |
| 576 + 1024 = 1600 | 2304 + 4096 = 6400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 | 147456 + 262144 = 409600 |
| 27 - 36 - 45 | 54 - 72 - 90 | 108 - 144 - 180 | 216 - 288 - 360 | 432 - 576 - 720 |
| 729 + 1296 = 2025 | 2915 + 5184 = 8100 | 11664 + 20736 = 32400 | 46656 + 82944 = 129600 | 186624 + 331776 = 518400 |
In order to illustrate the dynamics of the chart and the manner in which the multiples behave, let us take an example of numbers (a combination of the 3-4-5 triangle) as identified by Hugh Harleston in a structure in Urumchi, China. The reader is encouraged to read Mr. Harleston's work which treats the Urumchi structure in relation to the pyramid of Khufu and La pirámide del sol of Teotihuacan, Mexico. The numbers that Mr. Harleston offers for the Urumchi structure are: 216-288-360.
As we observe the chart offered here, these numbers appear within a more specific context, then simply as multiples of a 3-4-5 right triangle. The numbers obviously reflect the maya long count fractals (as Harleston himself has pointed out). But, now we may observe the different manners by which one may obtain these numbers within the different series of multiples themselves.
| 3 - 4 - 5 | 6 - 8 - 10 | 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 |
| 9 + 16 = 25 | 36 + 64 = 100 | 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 6400 |
| 9 - 12 - 15 | 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 |
| 81 + 144 = 225 | 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36854 = 57600 |
| 12 - 16 - 20 | 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 |
| 144 + 256 = 400 | 576 + 1024 = 1600 | 2304 + 4096 = 5400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 |
| 15 - 20 - 25 | 30 - 40 - 50 | 60 - 80 - 100 | 120 - 160 - 200 | 240 - 320 - 400 |
| 225 + 400 = 625 | 900 + 1600 = 2500 | 3600 + 6400 = 10000 | 14400 + 25600 = 40000 | 57600 + 102400 = 160000 |
| 18 - 24 - 30 | 36 - 48 - 60 | 72 - 96 - 120 | 144 - 192 - 240 | 288 - 384- 480 |
| 324 + 576 = 900 | 1296 + 2304 = 3600 | 5184 + 9216 = 14400 | 20736 + 36864 = 57600 | 82944 + 147456 = 230400 |
| 21 - 28 - 35 | 42 - 56 - 70 | 84 - 112 - 140 | 168 - 224 - 280 | 336 - 448 - 560 |
| 441 + 784 = 1225 | 1764 + 3136 = 4900 | 7056 + 12544 = 19600 | 28224 + 50176 = 78400 | 112896 + 200704 = 313600 |
| 24 - 32 - 40 | 48 - 64 - 80 | 96 - 128 - 160 | 192 - 256 - 320 | 384 - 512 - 640 |
| 576 + 1024 = 1600 | 2304 + 4096 = 6400 | 9216 + 16384 = 25600 | 36864 + 65536 = 102400 | 147456 + 262144 = 409600 |
| 27 - 36 - 45 | 54 - 72 - 90 | 108 - 144 - 180 | 216 - 288 - 360 | 432 - 576 - 720 |
| 729 + 1296 = 2025 | 2915 + 5184 = 8100 | 11664 + 20736 = 32400 | 46656 + 82944 = 129600 | 186624 + 331776 = 518400 |
Furthermore, one may observe how to visualize an interchange of multiples
which makes the system of computation extremely dynamic from different measurements
of a 3-4-5 right triangle.
It is impossible to even begin to offer computations that might appear to be meaningful for ancient reckoning systems in ancient China, Egypt, or Mesoamerica. But, the significant point is that the numbers related to these numbers easily refer to such systems of ancient reckoning. The number/fractal 1296000 has been cited as significant for ancient Egypt. The number 360c obviously refers to the ancient calendar day-count both in ancient Egypt and Mesoamerica. While the integer 72 has been significant in obtaining the Platonic Year: 72 x 360 = 25920. Too many combinations of related numbers become far too obvious to treat them at this juncture. Consider a few other examples:
| 1366560 | mayacompanion number |
| -466560 | Urumchi fractal derivative |
| 900000 | difference (a constant fractal of the maya system) |
| 46656 / 36 = 1296 fractal of ancient Egypt |
| 82944 / 36 = 2304 alautun (maya) |
Obviously, the system reflects a series of multiples, but it becomes evermore apparent that the system reflects the maya long count numbers/fractals precisely.
Multiples of the 3-4-5 Right Triangle and the Power of Three
Now, let us carry the numbers/fractals of the 3-4-5 right triangle to the power of three in order to observe their behaviour. It is here that there would seem to be an apparent extension of the Pythagorean theorem (x2 + y2 = z2) to involve the equation of the cube of the measurements of the 3-4-5 right triangle which derives from the series of multiples that we have chosen for the chart: w3 + x3 + y3 = z3.
This particular equation, derived from the 3-4-5 right triangle specifically, would also suggest the idea that Fermat's conjecture or the last theorem, in fact, may never have been even formulated had this equation been known at the time. For, if it is true that w3 + x3 + y3 = z3, then it would be quite apparent that a particular case of Fermat's Last Theorem, such as, x3 + y3 = z3 would represent an obvious impossibility. That could have been one line of reasoning for disregarding Fermat's Last Theorem as Frederich Gauss once commented.
We have presented the series of the 3-4-5 right triangle numbers alongside a graph for no other reason than to offer a visualization of the procedure. Since the numbers/fractals are proportional, the actual right triangle may be any given size; there is no apparent relationship between the number series and the graphlike figures. The idea is to simply show how one right triangle leads into another as of the first integer os each one.
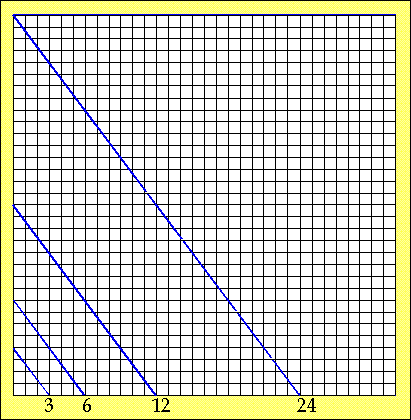
(Mediatio/Duplatio) to the Power of Three (n = 3)
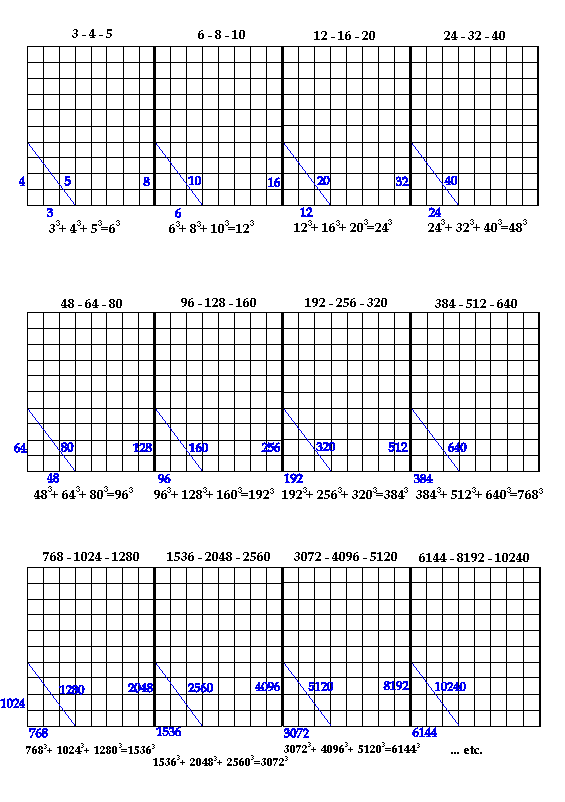
The sum of the cube of the integers of the 3-4-5 right triangle equals the cube of the initial integer's cube of the following right triangle of the series: for example,
| 3-4-5 | |
| 33 + 43 + 53 | equals 63 |
63 being the initial integer of the following right triangle on the progression of multiples of the 3-4-5 right triangle:
| 33 + 43 + 53 = 63 | |
| 63 + 83 + 103 =123 |
This procedure remains for the entire series of multiples of the 3-4-5 right triangle to infinity; in other words, an unending progression of 3-4-5 right triangles and their multiples/powers of there.
The most significant point possibly is that the numbers of this particular progression to the power of 3 do not reflect the maya long count numbers as such, but reflect rather constants that may be used to obtain the maya long count numbers:
| 256 | x | 36 | = | 9216 | maya fractal |
| 320 | x | 36 | = | 11520 | maya fractal |
| etc. |
Observe the numbers derived then from the cube of the numbers of the multiples
of the 3-4-5 right triangle in their progression:

The Cube of the 3-4-5 Right Triangle
Observations
From the numbers derived as of the multiples of the 3-4-5 right triangle, it becomes apparent that the maya long count positional level numbers/fractals may have been created as of a similar system of computation. The fact that this particular set of numbers occurs in ancient artwork around the world may also be a reason for a common mathematical heritage.
The behaviour of the numbers/fractals would seem to suggest a possible extension of the Pythagorean Theorem to include the cube of the integers related to the 3-4-5 right triangle and its multiples as illustrated in the various charts presented herein.
It may be further comprehensible how to evaluate Fermat's conjecture regarding the cube of certain numbers and their powers. Obviously Fermat was correct in surmising that it was impossible to find a relation of equivalency within the self-imposed terms of his conjecture. However, the reasons may be quite distinct from the ones that are suggested by his conjecture. The geometry of the 3-4-5 right triangle may be more helpful in understanding the reasoning behind the behaviour of whole numbers to the power of three.
For, it one understands that a progression of 3-4-5 right triangles and their multiples in whole numbers (which may be even fractals or fractions with the concept of a floating decimal place, which appears to have been the case in ancient reckoning systems), follows the equation w3 + x3 + y3 = z3, then one may comprehend this as an extension of the behaviour of the right triangle according to the Pythagorean Theorem (for the power of 2), and as a possible emendation to Fermat's conjecture regarding a possible (actually impossible) relation of equivalency of xn + yn = zn, specifically in the case of the power of three. If the maya understood the obvious concept of geometric progression of numbers implied in the equation cited to the third power for 3-4-5 right triangle, then they possibly would not have even entertained the idea forwarded by Fermat. Furthermore, they possibly understood the numerical possibility of
| x3 + y3 = z2 | , in other words, |
| 13 + 23 = 32 | |
| 1 + 8 = 9 | |
| 9 = 9 |
which would have probably discouraged them from considering again Fermat's conjecture given the knowledge suggested in the ancient reckoning system based on multiples of number sets of 1, 4, 8, 16, 32, 64, etc., and 9, 18, 36, 72, 144, etc. of the maya long count system.
The progression of numbers as reflected in the multiples/powers of the 3-4-5 right triangle would appear to be relevant to such visual expressions in the ancient artwork as the graphlike figures and designs of the ancient fretwork (grecas), especially among the cultures of Mesoamerica, such as the maya. It could be understood how the progression of triangles may have served as a basis for such designs of repeat, unending patterns as well.
©1996-2005 Copyrighted by Charles
W. Johnson. All Rights Reserved
Reproduction prohibited without written consent of the author.
email: johnson@earthmatrix.com
Earth/matriX
Science in Ancient Artwork Nº.56
THE MAYA LONG COUNT: AN EXTENSION OF THE PYTHAGOREAN
THEOREM
AND AN EMENDATION TO FERMAT'S LAST THEOREM
11 May 1996
1996-2005 Copyrighted by Charles W. Johnson. All
Rights Reserved.
Reproduction prohibited without written consent of the author.
| Home | Books | Author |