The Theoretical Interpretation of Spacetime/motion

Various ancient cultures based some of their artwork on the 3-4-5 right triangle, frequently referred to by geometrists as a perfect triangle. Pythagoras is cited as having understood the manner in which the three sides of a right triangle are related. This proposition has become known as the Pythagorean Theorem: the square of the hypotenuse of a right triangle equals the sum of the squares of the legs. This theorem may be expressed in different algebraic forms:

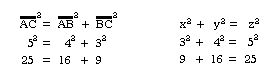
The first algebraic expression relates to the lines of geometry; the second to the mathematical one.

In our studies about Science in Ancient Artwork, we considered extending the Pythagorean Theorem to the power of three. The relation of equivalency among the terms of the equation vanish due to geometric progression. Yet, in the light of the positional level numbers/fractals of the maya long count system, it became obvious created a distinct relation of equivalency:

This expression reveals the relationship between right triangles adjacent to one another on a progression of multiples of the 3-4-5 numbers:

PROP.- In a progression of 3-4-5 right triangles, the cube of the shorter leg equals the sum of the cubes of the three sides of the right triangle inmediately preceding it on the progression.

By applying the ancient mediatio/duplatio method to the integers, the doubling/halving of the numbers in the equation produces a progression that reflects the numbers/fractals of the maya long count: 18, 36, 72, 144, 288, 576, 1152, 2304, etc. Multiples occur even two or three times within a single expression of the equation (in a right triangle's measurements). They occur in relation to the multiples of the constant number's progression; 1, 2, 4, 16, 32, 64, 128, etc. These two progressions form the basis of the numbers/fractals of the maya long count system as cited in the historical record.

By knowing one number on the progression cited, one may resolve all other unknowns to infinity on the progression in either direction simply by doubling/halving the integers in relation to the 3-4-5-6 relation. It could be stated that by knowing one maya numbers/fractal, all maya numbers/fractals may be known. The positional level numbers/fractals of the maya long count reflect a knowledge of the Pythagorean Theorem, as well as a knowledge of the possible extension of the Pythagoren Theorem to the power of three. Other powers may be easily involved in the computations as one derives distinct relationships on the progression of numbers.

Ancient monuments around the world, also in Egypt and China, appear to have been based on the 3-4-5 right triangle as of the telltale numbers/fractals found in this particular progression of values as explained by the extension of the Pythagorean Theorem to the power of three.

The research on Science in Ancient Artwork has led me to consider the Pythagorean Theorem in the light of the positional level numbers/fractals of the maya long count. Various essays deal with the possible extension of the Pythagorean Theorem to the third power (to the cube) in relation to the mathematical and geometrical appearance of the maya long count fractals within progressive series of right triangles.

It would appear that the 3-4-5 right triangle, and its multiples and variations, may have served as a basis for the ancient reckoning system of Mesoamerica. Extending the Pythagorean Theorem to the cube produces the exact series of multiples within the maya long count, something difficult to attribute to chance.

With the extension of the Pythagorean Theorem, not only is one able to achieve a translation between right triangles on a series of progression, but this is achieved through the maya long count numbers/fractals.

Enclosed for your review is an extract, "The Extension of the Pythagorean Theorem and the Maya Long Count". I would appreciate receiving your comments or critical observations. Thank you.

For a more detailed analysis of the extension of the Pythagorean Theorem, the maya long count numbers/fractals, and their relationship to such questions as Fermat's Last Theorem, consult the Earth/matriX books "Science in Ancient Artwork and Science Today".