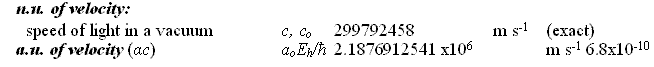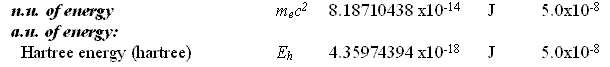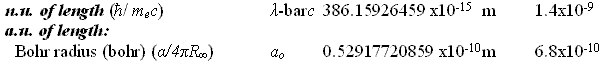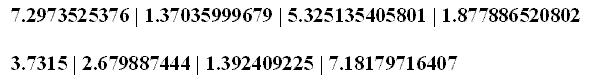Natural Units and Atomic Units

by Charles William Johnson

Abstract:
The author examines the mediating factors implied in the relationship of natural units
to atomic units as listed in the CODATA recommended fundamental physical constants.

At some point, the theme of natural units and Planck units must be analyzed in depth from a theoretical perspective. Before that may be accomplished, however, it is necessary to consider the fundamental physical constants that are expressed in the CODATA as natural units and atomic units.

In certain cases of physical constants, it would appear that there exists a conversion factor implied between the stated natural units and the atomic units as presented in Table VI, "The values in SI units of some non-SI units based on the 2006 CODATA adjustment of the values of the constants". [Published in "CODATA Recommended Values of the Fundamental Physical Constants: 2006", by Peter J. Mohr; Barry N. Taylor; and, David B. Newell, published in the CRC, 2009 - 2010 Handbook of Chemistry and Physics, Boca Raton, Florida, 2010: pages 1-9 and 1-10.]

The manner in which natural units and atomic units relate to one another may be obvious to some, but in my case, I have been unable to discern their exact relationship. Therefore, I present an elementary analysis of a possible relationship among some of the natural unit constants and some of the atomic unit constants as presented in the CODATA.

Essentially, Table VI of the CODATA presents the Quantity, Symbol, Numerical Value, Unit and Relative standard uncertainty of the natural units (n.u.) and the atomic units (a.u.) of certain fundamental physical constants. Several constants are repeated in both categories as shall be noted below.

The electron volt is presented outside of the natural units, but is presented within the atomic units as a.u. of charge: elementary charge (1.602176487). The concern in this analysis concentrates upon the mediation factor employed between the same nomenclature term presented as a natural unit and as an atomic unit, but with different numerical values. There is no apparent definition in the table that would suggest which are the numerical factors that serve as a conversion method between natural units and atomic units.

Each of the constants listed on the table present a symbol or symbolic formula identifying their derivation. However, that symbolic representation does not explain why or how the different numerical values are presented for apparently the same constant. For example, consider why the natural unit of energy is given a fractal numerical value of 8.18710438 while the atomic unit of energy appears with a fractal numerical value of 4.35974394. (Note that the numerical values appearing in the analytical part of this essay are written in their fractal form, with a floating decimal place, without reference to scientific notation, for purposes of comparison.)

Such a question as posed above may appear to a physicist or chemist as being unaware of the relationship between these different natural/atomic units. Yet, from the layperson's viewpoint, such a query seems valid in my mind. My first impression is that a certain ambiguity exists in the presentation of natural/atomic numerical values as some constants maintain the same value in both categories (mass, action), while others offer different values for the same nomenclature (velocity, energy, momentum, length, time). As mentioned, atomic unit of charge is somewhat of a hybrid, since it appears as an atomic unit, but not as a natural unit (electron volt).

For the sake of comparison, the order in which the natural units are presented is maintained in the order in which the atomic units are presented here. Although in Table VI of the CODATA, the order varies.

There are fifteen remaining atomic unit constants that are not treated in this analysis, and which have no apparent corresponding natural unit constant on Table VI.

Also listed together with the electron volt at the beginning of Table VI, is the (unified) atomic mass unit:

This particular constant does not appear to have relevancy for the analysis at this time in considering the relationship between natural units and atomic units.

I began my query about the relationship between the natural units and the atomic units because of an idea that has struck me throughout my studies of the CODATA recommended fundamental physical constants. The question that keeps arising in my mind is why some numerical values have their inverse expression listed in the CODATA and others do not. From the point of view of consistency and from that of how spacetime/motion exists in terms of matter-energy, I would suspect that if one inverse (reciprocal) relationship is significant then they are all significant. If one is listed, then all of them should be listed.

This idea arises when one considers the first two entries on Table VI and their possible relationship: the electron volt as of the (unified) atomic mass unit.

1.602176487 divided by 1.660538782 equals fractal 9.64853398 (the Faraday constant)

Yet, one does not find the inverse expression of 9.64853398 in the CODATA: fractal 1.036426883. Nevertheless, one does find for example such expressions as in the fine structure constant (7.2973525376) and the inverse fine structure constant (1.37035999679) which appear in the CODATA, but do not, however, appear on the list in Table VI of the CODATA. In the case of the cited example, one must ask why is e/u significant, yet u/e not apparently so. In my mind, they are both materially viable, i.e., they both exist.

The other question that arises in my mind, as I ponder the difference between the numerical values of the same category/event of matter-energy, concerns a possible conversion factor as they are expressed in either natural units and in atomic units. The symbolic expressions listed along side each particular constant have different numerical values that suggest the possibility that a conversion factor exists for deriving natural units from atomic units or deriving atomic units from natural units. A basic procedure in considering this aspect is to divide one of the units by the other. In this case, I began by dividing the numerical values of the natural units by those of the atomic units. [For a commonly held distinction between natural units and atomic units consider the citations at the end of this essay.]

Where the numerical values are the same in one set of constants or the other, there is no factor other than unit 1.0, if one wishes to make such an observation.

In these two cases, there is no analytical problem other than the question regarding the repetition of terms, a certain redundancy of values with different nomenclature. No matter which name is given to the constant, the numerical computations shall be the same since the numerical values are the same for each pair of values.

Now, consider each of the cited pairs for either natural units or atomic units that have the same nomenclature term but distinct numerical values. And, then, consider their relation of division between themselves.

The inverse fine structure constant [1.37035999679] mediates the natural unit of velocity with the atomic unit of velocity as follows.

299792458 divided by 2.1876912541 equals 1.37035999681 [ = inverse fine structure constant]

An unrecognized constant value [1.87788652101] mediates the natural unit of energy with the atomic unit of energy as follows.

8.18710438 divided by 4.35974394 equals 1.87788652101

The inverse fine structure constant [1.37035999679] mediates the natural unit of momentum with the atomic unit of momentum as follows.

2.73092406 divided by 1.992851565 equals 1.37035999467 [= inverse fine structure constant]

The fine structure constant [7.297352537516] mediates the natural unit of length with the atomic unit of length as follows.

3.8615926459 divided by 5.2917720859 equals 7.297352537516 [= fine structure constant]

An unrecognized constant value [5.32513540596] mediates the natural unit of time with the atomic unit of time as follows.

1.2880886570 divided by 2.418884326505 equals 5.32513540596

From the previous computations, it becomes obvious that the fine structure constant and its inverse expression are conversion factors between some of the fundamental physical constants expressed as natural units and/or atomic units. However, at first glance, it was not obvious to me at least, what the significance of the numerical values of 1.87788652101 and 5.32513540596 represented as they do not appear elsewhere in the CODATA listing of fundamental constants.

It did not take long, however, to find out what those two numerical values represent. Consider the following computation that involves the fine structure constant and its inverse expression.

Now consider the following computation, whereby the fine structure constant is divided by its inverse expression:

7.2973525376 divided by 1.37035999679 equals 5.325135405801

Then consider when the inverse fine structure constant is divided by the fine structure constant per se.

1.37035999679 divided by 7.2973525376 equals 1.877886520802

Therefore, the conversion factor for n.u.|a.u. of energy and time is the ratio between the fine structure constant and the inverse fine structure constant [5.325135405801 | 1.877886520802].

Of the five fundamental physical constants that maintain the same term nomenclature but present different numerical values for either their natural unit expression or their atomic unit expression, three pairs are based on the fine structure constant and its inverse expression; and, two pairs are based on the ratio of the fine structure constant and its inverse expression.

Note further, the two values derived thereof said ratio are themselves reciprocal expressions of one another.

1 divided by 5.325135405801 equals 1.877886520802

The conversion factors, then, for the seven repeat fundamental constants as natural and atomic units, are: a) the unit 1.0, b) the fine structure constant and its inverse expression, and, c) the ratio of these latter two expressions.

One may question whether it is a valid procedure to employ the fine structure constant and its inverse expression as a conversion factor as of the natural units. More significantly, one must question whether it is valid to employ the ratio of these two constants as a conversion factor between the natural units and the atomic units.

Let me illustrate the query by using a similar procedure with an apparently unrelated numerical value, as in the boiling point of water [373.15 kelvin].

Take an apparently constant value [3.7315] and find its reciprocal expression [2.679887444].

1 divided by 3.7315 equals 2.679887444

Now, divide the first value by the second, as was done in the previous relationship for the fine structure constant and its inverse expression.

3.7315 divided by 2.679887444 equals 1.392409225

1 divided by 1.392409225 equals 7.181796716407

The numerical values 1.392409225 and 7.181796716407 thus represent the ratio of the boiling point of water to its own reciprocal. According to the computational procedure, these numbers would serve in the same capacity as the numerical values derived above regarding the conversion between natural units and atomic units:

The first set of numerical values would be relational in procedural terms as the second numerical values. Computationally 7.2973525376 is to 3.7315 as 1.37035999679 is to 2.679887444; and so on for the two sets of numbers. In terms of general logic, a ratio resulting from two constant values must represent a constant value in itself.

In such case, if the ratio of numerical values between a constant and its inverse expression represent correct measurements, then they should be listed in the CODATA with their corresponding explanation, along side the other derived constants reflecting ratios. The question remains, however, whether it is possible to have the ratio [inverse or not] of a pair of constants [inverse or not fine structure constant] set as a conversion factor for deriving natural and atomic units.

In summary, in their conversions, the natural/atomic units of momentum, length and velocity employ the fine structure constant and its inverse expression. While the natural/atomic units of energy and time employ the ratio of the fine structure constant and its inverse expression. And, the natural/atomic units of charge and mass employ unit 1.0. The question remains whether the computational procedure is valid if based upon distinct conversion factors or relationships. In other words, how does one know which particular conversion factor to employ for which particular pairs of natural/atomic constant units.

From here, one would have to analyze the remaining atomic unit constants as of their symbolic formulae which present multiples [powers greater than 1] of some of the cited terms. Such an analysis would question why, for example, a particular term is taken to the second, third, fourth or fifth powers.

One of the analytical purposes behind deriving natural units is to find the minimum expression of matter-energy in terms of its units of measurement. Yet, the cited symbolic formulae present an apparent theoretical contradiction in that they express multiples or powers of some of the terms. Consider a single example in this regard.

a.u. of electric polarizability times a.u. of first polarizability

1.6487772536 times 3.206361533 equals 5.286575962428 halves to 2.5813359191 [near the von Klitzing constant 2.5812807557].

This becomes more obvious is one limits the number of decimal places in order to comprehend the fractal multiples occurring within these values.

1.6487 times 3.2064 equals 5.28639168 halves to 2.581245938.

This value is somewhat low for the von Klitzing constant, but adjustments may be made accordingly. The idea is to illustrate how certain constants together produce fractal multiples of other constants, which apparently are part of their original terms. Additional examples of the relationship of multiples among pairs of constants have been forwarded in some of my previous essays on the Planck constants.

Inasmuch as the measurements of the fundamental physical constants are correct, then one may find relationships infinitely so. For the identified fundamental physical constants reflect a specific aspect of spacetime/motion in its varied forms of matter-energy, which are relational from the outset. In searching for the minimum expression of the natural units, then, one would expect to view the analysis upon the minimum expression of the numerical values of the different physical constants.

Now, whether it is possible to derive minimum natural units, and/or atomic units, as illustrated in the literature, constitutes another level of analysis. With the idea of physical quanta arises the idea of a minimum expression of a unit of measurement. That particular subject remains to be discussed. To date, I have only been attempting to consider the internal logic of the fundamental physical constants as of their numerical expressions presented in the literature. One must still analyze existing relationships of the terms before attempting to analyze the defining concept of a natural unit of matter-energy.

In my view, the varied numerical relationships among the different pairs of natural/atomic units of certain constants, as analyzed in this essay, do not afford a theoretical understanding of the concept of natural units. In order to comprehend the theoretical conceptualization of natural units, one would have to venture beyond the numerical values of the fundamental physical constants.

-0-

Citations:

"Natural units are intended to elegantly simplify particular algebraic expressions appearing in physical law or to normalize some chosen physical quantities that are properties of universal elementary particles and that may be reasonably believed to be constant. However, what may be believed and forced to be constant in one system of natural units can very well be allowed or even assumed to vary in another natural unit system.

"Natural units are natural because the origin of their definition comes only from properties of nature and not from any human construct. Planck units are often, without qualification, called "natural units", when in fact they are only one of several systems of natural units, albeit the best known such system. Planck units might be considered unique in that the set of units are not based on properties of any prototype, object, or particle but are solely derived from the properties of free space.

"As with any set of base units or fundamental units the base units of a set of natural units will include definitions and values for length, mass, time, temperature, and electric charge. Some physicists do not recognize temperature as a fundamental physical quantity, since it simply expresses the energy per degree of freedom of a particle, which can be expressed in terms of energy (or mass, length, and time). Virtually every system of natural units normalizes Boltzmann's constant k_B to 1, which can be thought of as simply a way of defining the unit temperature." [Source: www.wikipedia. com, under Natural Units].

-0-

"Atomic Units {Hartree}... First proposed by Douglas Hartree to simplify the physics of the Hydrogen atom. Duff calls these "Bohr units". The unit energy in this system is the total energy of the electron in the first circular orbit of the Bohr atom and called the Hartree energy, E_h. The unit velocity is the velocity of that electron, the unit mass is the electron mass, me, and the unit length is the Bohr radius, . They can be obtained from "Schrödinger" units with the substitution:

This removes the speed of light (as well as the gravitational constant) from the definitions and its numerical value in atomic units is the reciprocal of the fine-structure constant, 1/?. Hence any observed variation over space or time in the value of ? is attributed to variation in the speed of light." [Source: Wikipedia.com, under Natural Units]

March, 2010 ©Copyrighted by Charles William Johnson. All rights reserved.
Reproduction prohibited.

Earth/matriX: SCIENCE TODAY

johnson@earthmatrix.com

Our Price $17.95 Paperback In Stock   Our Price $8.99 Purchase in Amazon   Our Price $18.95 Paperback In Stock The physics paradigm today is based mainly upon the concept of c-square, the squaring of the speed of light in a vacuum. Numerous fundamental physical and chemical constants provided in the physics literature [CODATA] reflect numerical values based upon powers of c, the speed of light in vacuo. The speed of light in a vacuum is determined to represent the upper limit of movement of mass|energy by physicists.   The upper speed limit for a light photon is 299792458 meters/second. The square of that number produces a numerical value that does not exist in any form of matter-energy. The c-square actually represents a number that corresponds to a near massless event: a light photon. The author goes beyond a critique of Albert Einstein’s famous formula based upon this unreal number. The rejection of Einstein’s formula is explored through basic math, the summation of powers in the equation’s terms.   A common procedure followed in deriving many of the CODATA recommendations is to divide certain fundamental physical constants by the value of the elementary charge, e, 1.602176487. With regard to the Planck constants and units of measurement, the case is argued that Max Planck may have simply reversed engineered this procedure in order to derive his natural units.