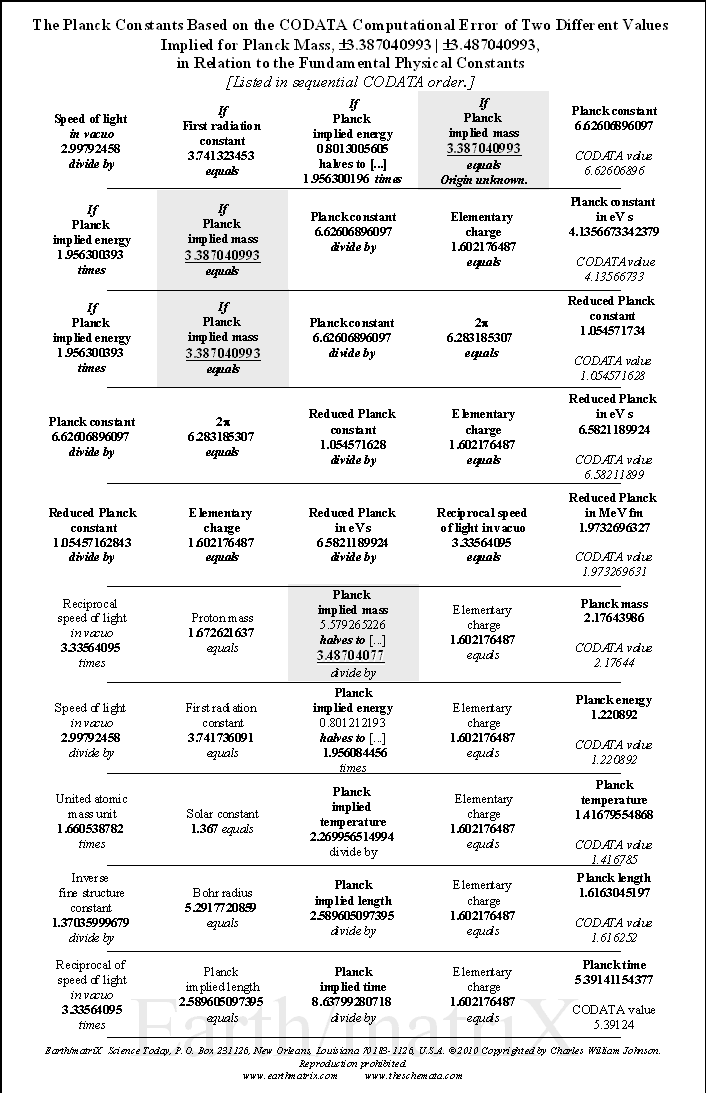
Proposal to Include Planck Implied Values in the CODATA Listing

by Charles William Johnson

After having analyzed different interrelationships among the CODATA fundamental physical constants, it has become apparent that certain numerical values must be included in the CODATA recommended values.

The main thrust of my analysis to date has been in relation to the Planck constants of mass, energy, temperature, length and time. In a previous analysis, I have illustrated how one may derive Planck implied values, that is, numerical values as of the Planck constants. The manner in which the Planck implied values are generated is by multiplying each Planck constant times the elementary charge [1.602176487].

The Planck implied values are as follows:

If one reverses this procedure, and then divides the Planck implied numbers by the elementary charge, then one would realize that Planck mass, energy, temperature, length and time are actually reduced numerical values, as they have been divided by the elementary charge. For, I shall not concern myself with this discussion and simply accept the Planck implied numerical values as that, values that are implied from the computations in the manner shown.

For each one of the Planck implied values there exist certain pairs of fundamental physical constants that through basic math produce the Planck values. From my analytical perspective the cited Planck implied values are the Planck values. And, the Planck values published in the CODATA today are the reduced Planck values. The reduction comes from the fact that the corresponding numerical values are derived as of the division of the Planck values by factors such as the elementary charge, pi or the inverse of the speed of light in vacuo. In order to detail this line of reasoning it would be necessary to write various tomes on the subject.

For now, the purpose of this essay is to suggest the inclusion of the Planck implied values or, simply put, the cited Planck values, within the listing of the CODATA's recommended values for the fundamental physical constants.

As may be viewed from the numerous pairs of fundamental physical constants that produce the Planck implied values, these are essential to understanding the interrelationships among the Planck constants and the other fundamental physical constants, as well as, essential to the general understanding of the fundamental physical constants themselves.

In order to understand how the CODATA fundamental physical constants relate to one another, it is necessary to discern the ratios and products as of these derived Planck implied values. Without explicitly illustrating the Planck implied values, it would appear that each of the CODATA fundamental physical constants exist either independently of the other constants or at best as of its inverse expression.

Yet, by knowing the Planck implied values derived as of the interrelationships of the fundamental physical constants, one is thus able to illustrate the series of fractal multiples of particular numerical values shared by different constants. By examining, then, the pairs of physical constants in relation to one another, it is possible to understand that such pairings essentially demonstrate a mathematical procedure based upon the fractal multiples of a particular numerical value.

For example, understanding that certain pairs of elements derive the same/similar numerical value represents understanding firstly the fractal multiple series involved, as in, say for example the numerical value 144:

Secondly, each one of the terms of the different equations that derive the same/similar numerical value [144 in the case of this basic example] represent, if correctly measured, a specific spacetime/motion event in the form of matter-energy. Hence, just because an apparent redundancy exists within the fundamental physical constants [the different terms to the different equations], does not mean that they do not exist or that they are insignificant. On the contrary, if reflexive of matter-energy events, then they represent the interrelated nature of spacetime/motion. In other words, all of the fundamental physical constants exist, whereby each one represents a particular aspect/form of matter-energy.

What may possibly be deemed as confusing is the general practice in physics of assigning a particular, accidental name to identify a given constant [i.e., Planck, Wein, Boltzmann, Josephson, von Klitzing, and so on]. Imagine any one of the terms cited in deriving the example 144 being assigned a particular name in order to identify its relationship to that particular equation. The problem comes from comparing a particular equation to derive 11 with other equations that derive the same/similar value [144]. That would obviously make it difficult to discern how all of those numbers relate to the 144 derived value. So it occurs with many of the fundamental physical constants being assigned a person's name. It becomes difficult to understand how all of those physical constants are related to one another vis-a-vis the shared common derivative numerical value [such as 3.4870409933; 1.956084456; 2.269939614; 2.589520951; 8.637717964, which are analogous to the 144c].

In exploring the interrelationship among the different fundamental physical constants, I have maintained the proper names of the constants along with their respective numerical values. At this stage of the analysis, there is no commentary regarding the nature of each of the physical constants in terms of what each one represents as of spacetime/motion, or matter-energy. The purpose at this juncture is to merely comprehend how the nominal constants function as of their numerical values in relation to the concept of fractal multiples.

By exploring the interrelationships of the CODATA recommended values it is possible to distinguish series of fractal multiples and later compare these in relationship to the perceived representations of forms of matter-energy. With regard to the Planck constants, by comparing these interrelationships it is possible to derive the numerical values of the Planck constants as of the CODATA recommended values without the use of the symbolic formula of each of the fundamental physical constants.

In my view, this is the most significant part of the exercise in comparing the names of constants to their corresponding numerical values. My suspicions is that all of the fundamental physical constants share an explanation as of basic math without the need to recur to algebra or calculus as such, at least in this initial stage of comparison.

Placing aside for the moment, any observations about the perceived errors within some of the listings of the symbolic formulae, I should like to concentrate upon the recommendations for including the Planck implied values into the body of the CODATA listing. In my view, it is next to impossible to comprehend the entire listing of the CODATA fundamental physical constants without understanding the interrelationships illustrated on the tables presented here and in a previous essay on my web-site [www.earthmatrix.com].

Once all of the comparative interrelationships are fully discerned, then it is possible to question the significance of those interrelationships and ask the relevant interrogatories as to why specific fundamental physical constants relate to one another in the manner that they do. This means discerning why certain pairs of constants produce the same/similar derivative numerical value. In my analysis, at least, I have not reached that stage of inquiry, and simply provide a comparative view of the fractal multiple numerical values of different pairs of constants.

A next-step in my analysis would be to consider why the different pairs of fundamental physical constants produce the same/similar numerical values, as cited in the Planck implied values. But, that analysis must wait until I am able to present more cases of similarly structured comparative analyses of the pairs of constants. One must examine first the manner in which the Planck constants relate to the CODATA fundamental physical constants. Hence, the purpose of this brief commentary, as well as the previous essay and book on the same subject.

The tables presented in this essay come from the previous essay that I wrote about the Planck constants being based upon the CODATA fundamental physical constants. The first table presented here illustrates limited examples for each of the Planck implied values, cited above. The second table presents seven different pairs of fundamental physical constants that produce the Planck implied value for energy of ca. 1.956084456, with slight variations. The third table presented here offers insight into seven different pairs of fundamental physical constants that produce the Planck implied value for length of ca. 2.5896051.

From these tables, an explicit recognition is required as to the significance of the Planck implied values, and in my view, the fact that so many pairs of CODATA recommended numerical values for the fundamental physical constants relate as described, causes me to suggest their inclusion in the CODATA listing.

It is necessary to compute as many pairs of interrelationships as possible in order to comprehend the complexity of how spacetime/motion exists in the specific forms of matter-energy events listed in the CODATA. For the time being, I am forwarding the pairs of interrelationships that I have been able to discern, knowing that uncountable ones remain to be specified.

Mainly, it is necessary to consider Planck implied temperature and Planck implied time. I have computed a few of these implied numerical values, but many more remain to be identified. The suggestion to include the Planck implied values in the CODATA listing, however, appears to be substantiated in my mind as of the pairs that have already been identified.

Earth/matriX Editions New Orleans, Louisiana P.O. Box 231126, 70183-1126 USA February,
© 2010- Copyrighted by Charles William Johnson. All rights reserved. Reproduction prohibited.

Our Price $17.95 Paperback In Stock   Our Price $8.99 Purchase in Amazon   Our Price $18.95 Paperback In Stock The physics paradigm today is based mainly upon the concept of c-square, the squaring of the speed of light in a vacuum. Numerous fundamental physical and chemical constants provided in the physics literature [CODATA] reflect numerical values based upon powers of c, the speed of light in vacuo. The speed of light in a vacuum is determined to represent the upper limit of movement of mass|energy by physicists.   The upper speed limit for a light photon is 299792458 meters/second. The square of that number produces a numerical value that does not exist in any form of matter-energy. The c-square actually represents a number that corresponds to a near massless event: a light photon. The author goes beyond a critique of Albert Einstein’s famous formula based upon this unreal number. The rejection of Einstein’s formula is explored through basic math, the summation of powers in the equation’s terms.   A common procedure followed in deriving many of the CODATA recommendations is to divide certain fundamental physical constants by the value of the elementary charge, e, 1.602176487. With regard to the Planck constants and units of measurement, the case is argued that Max Planck may have simply reversed engineered this procedure in order to derive his natural units.