
Science in Ancient Artwork and Science Today
The Theoretical Interpretation of Spacetime/motion
Dedicated to the preservation of human knowledge in the arts and sciences, and to the
advancement of human survival and to that of our planet in a world threatened by our own development.
The Planck Constants Based on the Fundamental Physical
Constants By Charles William Johnson
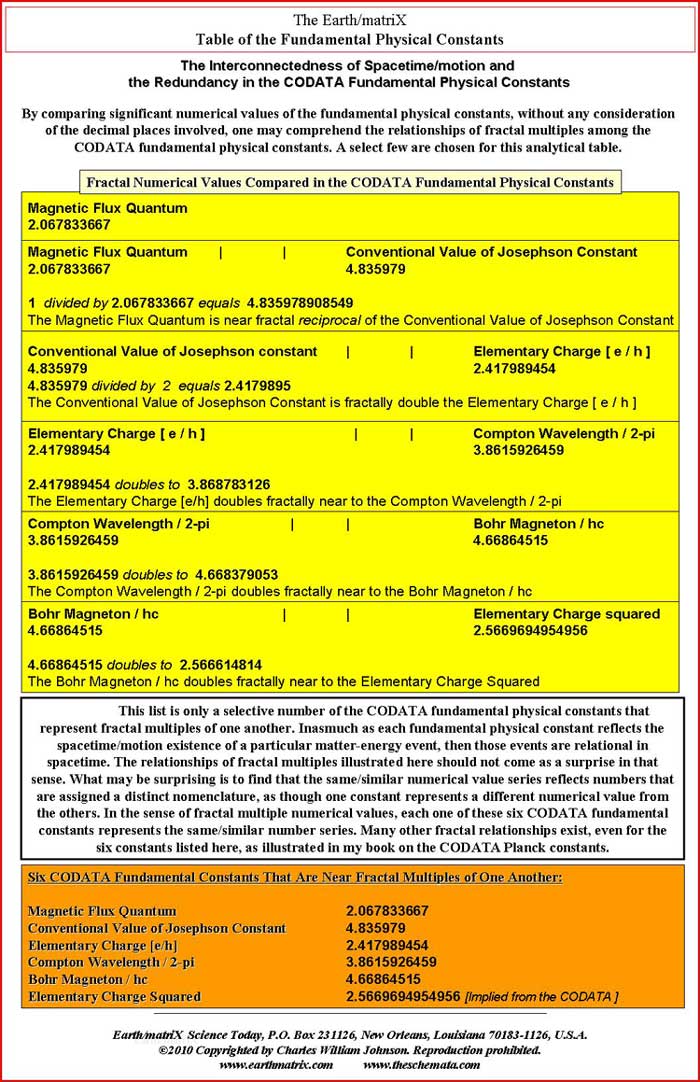
The 2006 CODATA recommendations for the fundamental physical constants, as one may observe from the list below, are often based upon specified symbolic formulae. The defining Planck constant 6.62606896 together with two other constants have no corresponding symbolic formulae listed in the CODATA. Many physicists mention that Max Planck, who created the Planck constant in 1899, never disclosed how he derived the numerical value of his constant. For nearly 110 years now, physicists appear to have uncritically accepted Planck's constant, originally given a value of 6.885 by Planck in 1899, which he later changed in 1900 to 6.55. Such an unquestioning acceptance of a thesis is not common within the field of physics, but supposedly Planck's values in experimentally measuring the energy in a relationship of frequency|waves worked well, and therefore it was accepted. Evidently it continues to be accepted, as the constant carries Planck's name, even though over the decades the numerical value has changed, finally resting at the current 6.62606896 fractal value.
Ultimately, it is impossible to question the symbolic formula of all the Planck constants inasmuch as three out of the ten constants provided in the CODATA have no symbolic formula listed for them. Planck's constant, the first one listed by the CODATA appears without an obvious theoretical basis, as it lacks a symbolic formula. Its derivation is thus unknown, or at least undisclosed. No one apparently knows how it was theoretically derived but only that it works empirically. Hence, I sought to understand how Max Planck may have derived the numerical values of his constants. Not sharing confidence, however, in the symbolic formulae given for the rest of the Planck constants, I decided to seek a possible derivation of the Planck constants as of the other fundamental physical constants. One analytical purpose that I had in my mind was to avoid any reference to the symbolic formulae that contain square roots. Four of the ten Planck constants contain formulae with square root expressions. For although they have their symbolic formulae expressed to the power of 0.5 that essentially means employing the square root procedure. Square roots produce two possible answers to every resolution depending upon where the decimal place lies in the numerical values of the terms involved in the computations. The fundamental physical constants, even those with square root expressions, present a single constant or answer as though that were the only possible answer. Now, to move along, consider the original general values forwarded by Max Planck in his 1899 lecture in Berlin:
Further, Planck provided the following specific data:
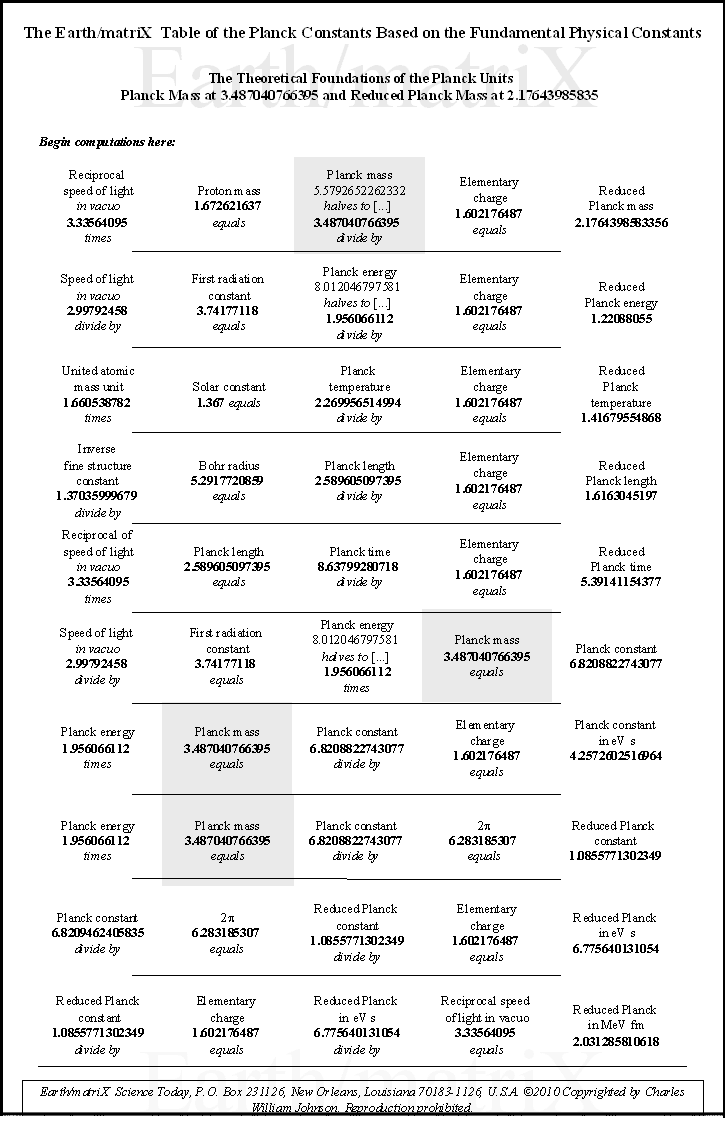
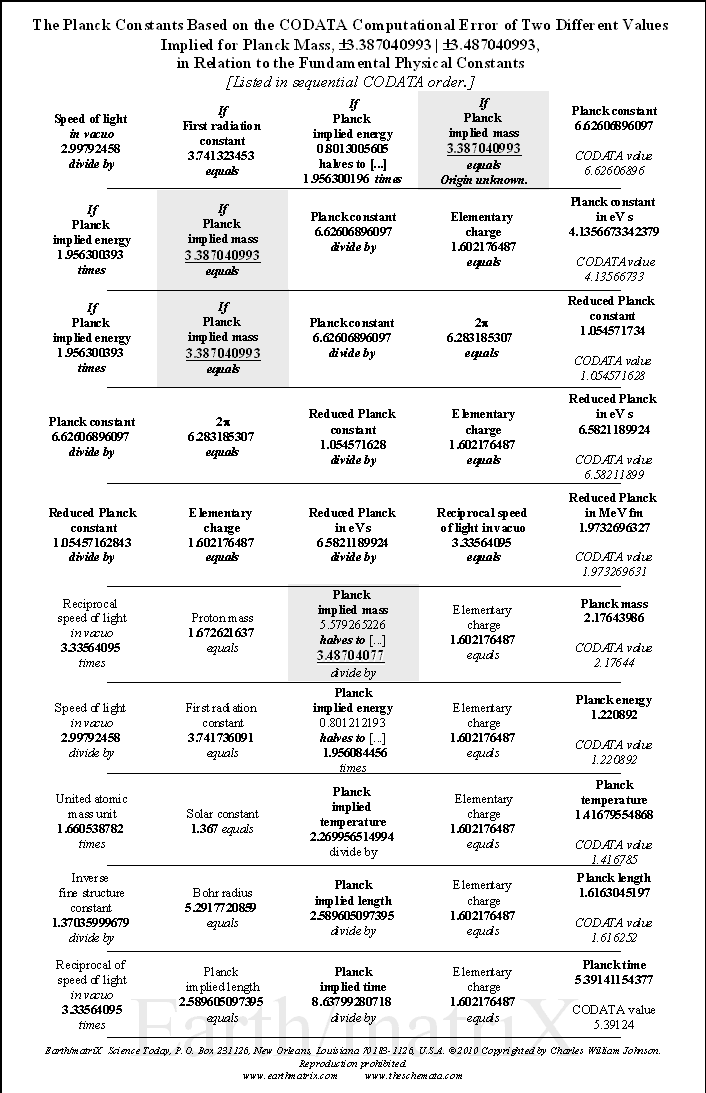
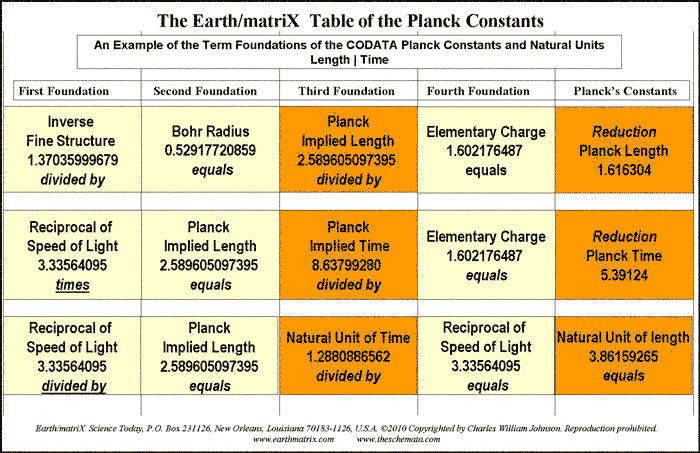
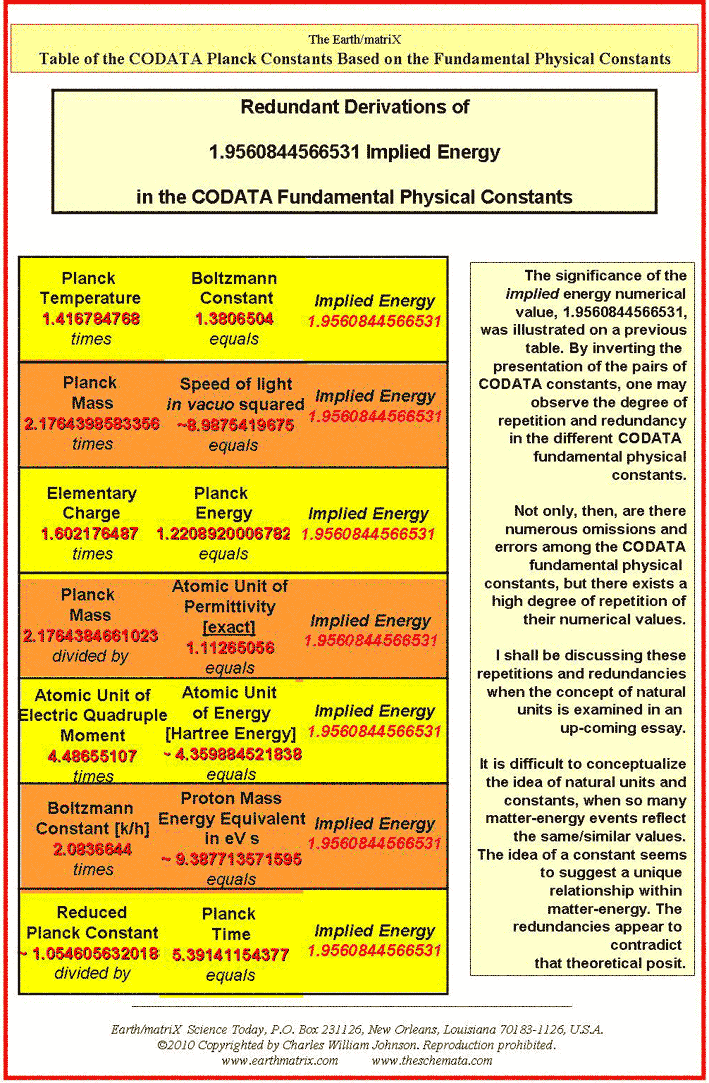
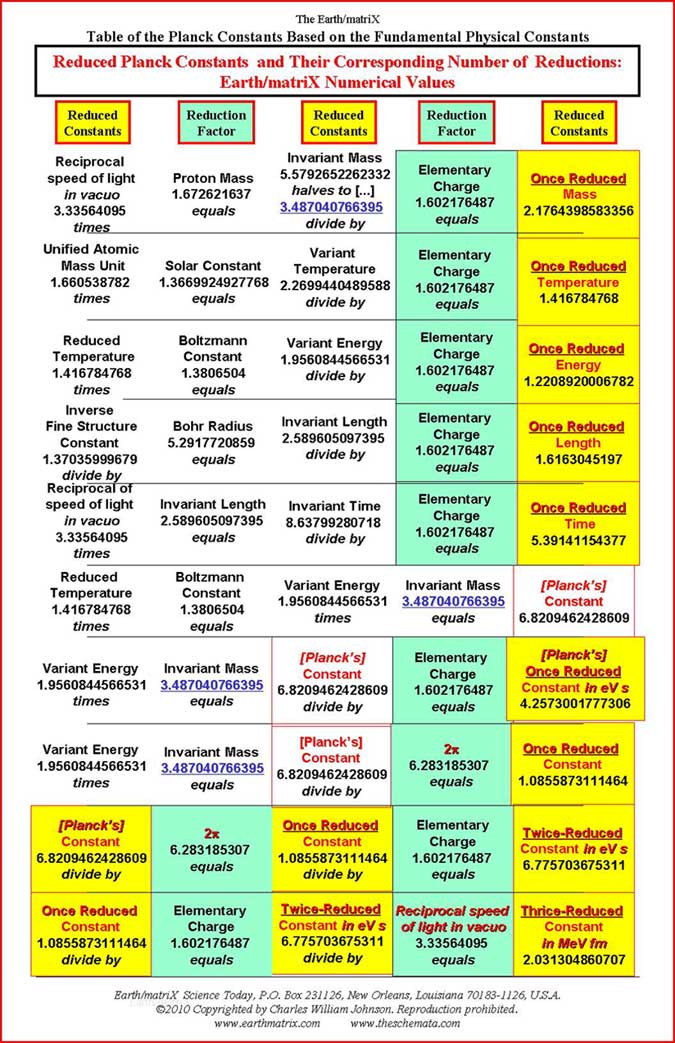
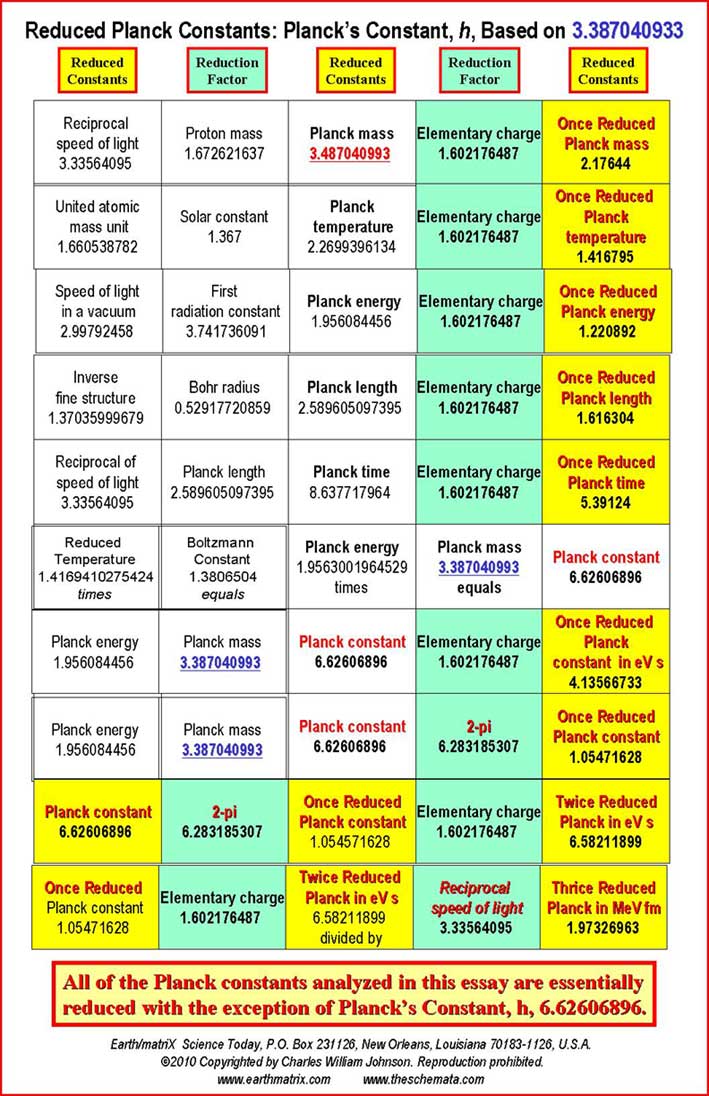
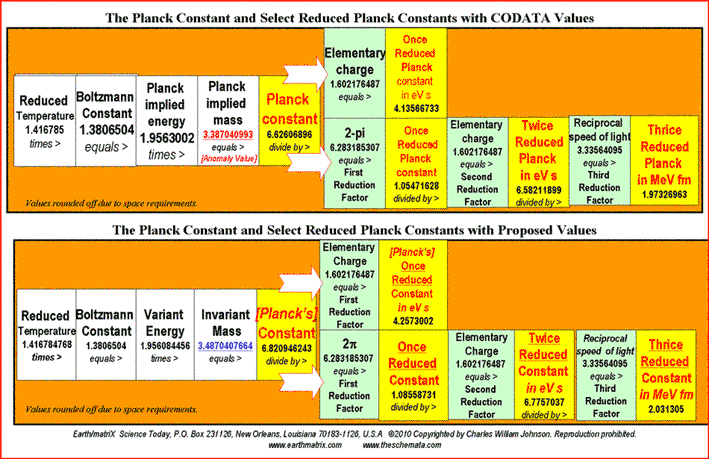
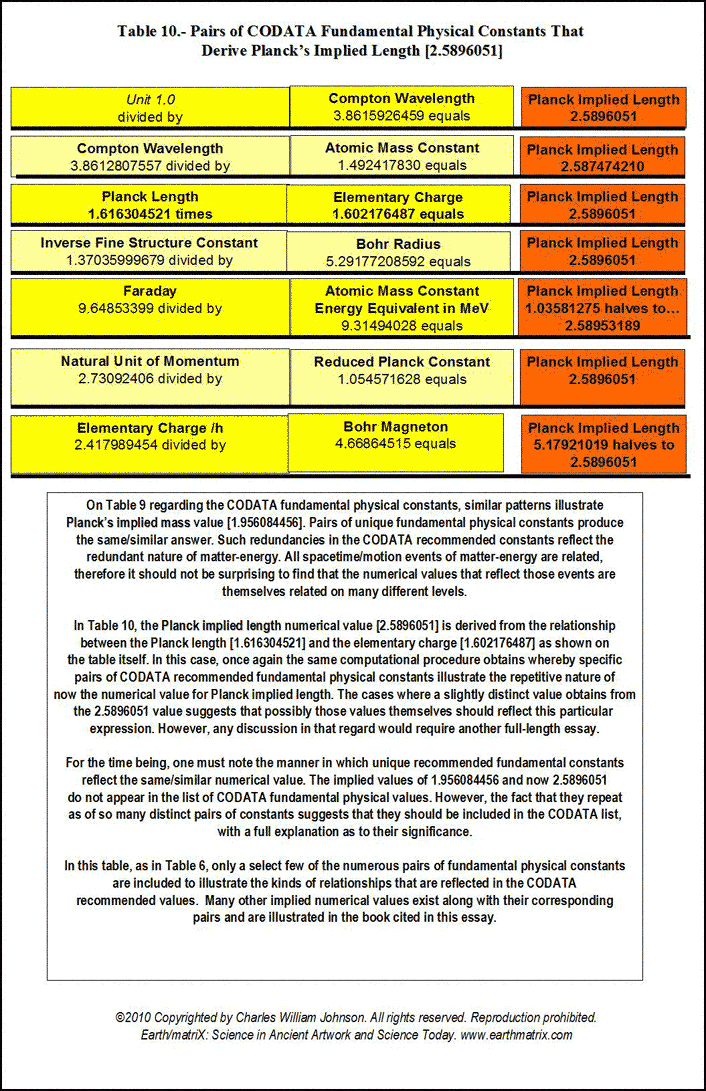
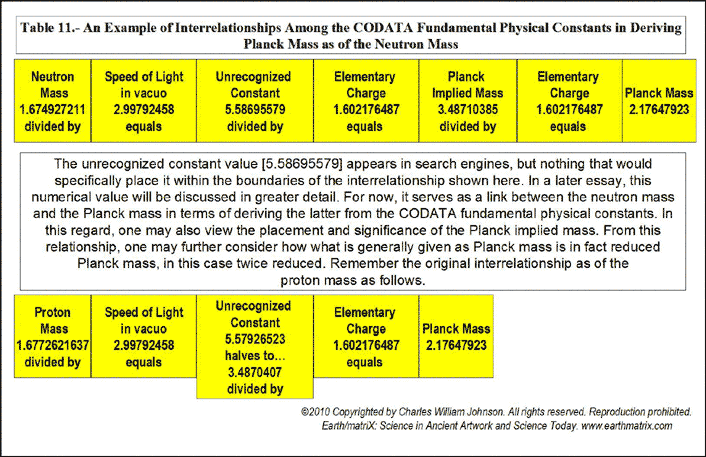
Notice that in general the CODATA follow the sequential order listed by Max Planck in his published lecture; first, the general Planck constants; then, secondly, the specific ones. From my studies, the order of the Planck constants should be reversed. First the specific constant measurements must be presented, followed by the general theoretical constants. Such is the order presented in Table I of the attached Earth/matriX Table of the Planck Constants Based on the Fundamental Physical Constants. The reason for inverting the order is computational. One must first derive the specified numerical values, and then proceed from there in order to be able to derive the generally posited matter-energy relationships. After the specific constant values are derived it is then possible to derive the general theoretical Planck constants; not before. The requirements of this procedure become clear through the computations on Table I. As a methodological procedure, I began my research by multiplying the CODATA numerical values for the Planck constants by the elementary charge [1.602176487]. The results from that computation were then compared against the numerical values of the CODATA fundamental physical constants. It soon became clear that for some of those results there were two fundamental physical constants whose numerical values in relationship to one another could produce that same numerical value resulting from the Planck constants being divided by the elementary charge. By reverse engineering the Planck constants' numerical values in this manner it is possible to identify the three main fundamental physical constants that derive some of the Planck constants. Essentially that is the information presented in Table I. The three fundamental physical constants that derive certain Planck constants are listed in the first, second and fourth columns of the cited table. The third column of the table contains eight Planck constants and two reduced Planck constants. On the fifth and last column of the table are listed the ten reduced Planck constants, repeating the two that appear in column three. The two reduced Planck constants that appear in column three are thus twice reduced by the time they appear on the fifth column. The theoretical concept of "reduction" may not be the best of terms, but I have retained its use for now in order to be able to compare the implied values that I have derived from the CODATA Planck constants against the given CODATA values. The theoretical concept of "implied values" is itself not the best of terms either, but it draws attention to the fact that some of the fractal numerical values presented on the table are derived from the standing CODATA values, meaning the given CODATA values imply the existence of still other values. Simply put, the CODATA numerical values imply a prior set of numerical values; in fact, they require them. Essentially this is what I have done, take the CODATA numerical values and work backwards from them in order to see which numerical values of a particular fundamental physical constant produce the CODATA values. Enter Table I, the Earth/matriX Table of the Planck Constants Based on the Fundamental Physical Constants. The theoretical foundations of the Planck units are presented in detail in Table I. Errors and omissions that I consider to exist in the CODATA are presented in Table II. The entire critical analysis of the CODATA may be examined in my book, Errors and Omissions in the CODATA and, The Planck Constants Based on the Fundamental Physical Constants [Earth/matriX Editions, 2010]. A word of caution is required here. The fractal values presented on the Earth/matriX tables of the Planck constants and fundamental physical constants may vary distinctively as of the baseline fractal values used; be they from the CODATA or from other sources. Further, using the same fractal values of two fundamental constants may produce different values in their mantissas depending upon whether they are divided or multiplied by one another. The first computation on the table that follows employs multiplying the reciprocal of the speed of light in vacuo times the proton mass. A similar result could be obtained inversely by dividing the proton mass by the speed of light in vacuo, yet the numerical result would differ slightly. In this summary and in my book the choice of employing either multiplication or division lies at times with the needs of illustrating a particular numerical value. Moving along, there are five computational steps in the derivation of each of the ten cited Planck constants. One begins on the first row of Table I, by multiplying the reciprocal of the speed of light by the proton's mass. This step derives the first Planck constant fractal value, which is 5.5792652262332 and which must be halved to fractal multiple 3.487040766395. This latter value is considered to be Planck mass. The reason for this lies within the initial analytical procedure where I multiplied the Planck constants by the elementary charge: Planck mass 2.17644 times 1.602176487 equals fractal 3.4870409933662. Therefore, in inverse order, after obtaining the 3.487040766395 numerical value from the first computation on the table, this value is divided by the elementary charge figure in order to derive the reduced Planck mass: 2.1764398583356, which is referred to in the CODATA as Planck mass. As shown, however, this is actually a reduced form of mass since it obtains from the division by the elementary charge. The constant Planck mass, 3.487040766395 defines the five general Planck constants listed last on Table I. Without this value it is impossible to derive the Planck constant and the subsequent [reduced] Planck constants. On Table II, where the five general Planck constants appear first, the analytical dilemma becomes obvious in that there appears a similar but distinct value of 3.387040993, whose origin is not only unknown, but not recognized in the CODATA. Nonetheless, the 3.387040993 fractal value is implied in and required by the CODATA in order to theoretically produce the Planck constant, 6.62606896. Table I and II essentially points out the anomaly of 3.387040993 and its contradiction to the 3.487040993 value for Planck implied mass. Briefly, Table II illustrates how there exist two different implied numerical values for Planck implied mass in the CODATA.; that is the only manner in which the set of CODATA Planck constant numerical values can be produced. Returning to Table I, on its second row, the speed of light in vacuo is divided by the first radiation constant in order to produce Planck energy, 1.956066112. This Planck energy value is in turn divided by the elementary charge in order to produce the reduced Planck energy fractal value, 1.22088055. The Planck energy value, 1.956066112 represents a serious omission from the CODATA even though it is implied and is mandatory in deriving the CODATA value of 1.220892 for Planck energy. Again, the CODATA Planck energy is in fact a reduced value for energy. In other words, some of the constants that the CODATA identifies as Planck constants are actually reduced Planck constants. The third row on the Earth/matriX Table I proposes the unified atomic mass unit times the solar constant in order to derive Planck temperature, 2.269956514994. By dividing Planck temperature by the elementary charge, one obtains the reduced Planck temperature fractal value of 1.41679554868; again, incorrectly presented by the CODATA as Planck temperature. The computational procedure is obvious and the reduction fractal value is evident; I state this again for emphasis. The fourth row on Table I treats the inverse fine structure constant divided by the Bohr radius thus deriving Planck length, 2.589605097395. Following the same systematic procedure, that value is thus divided by the elementary constant and obtains the reduced Planck length fractal value, 1.6163045197. Once again, what the CODATA identifies as Planck length is in fact reduced Planck length. The final specific Planck constant appears on the fifth row of Table I, and involves multiplying the reciprocal of the speed of light in vacuo by the Planck length, in order to derive Planck time, 8.63799280718. This fractal value is then divided by the elementary charge value in order to obtain the reduced Planck time value, 5.39141154377. The CODATA's Planck time is in fact reduced Planck time. In summary, this first section of Table I, regarding the specific Planck constants, demonstrates that the CODATA Planck constants for mass, energy, temperature, length and time are in fact reduced Planck constants. This occurs because of the fact that the specific CODATA Planck constants are derived by the division of the elementary charge, thus effectively reducing their values. It is important to emphasize that the two fundamental physical constants in the first and second columns produce the numerical values of the third column; meaning that these latter values of the table's third column represent the Planck constants. As far as I can tell so far, no two fundamental physical constants produce the values of the fifth column ---with the exception of the Planck constant, 6.62606896. Nine of the values in the fifth column are produced by the combination of a Planck constant together with the elementary charge, 2-pi or the reciprocal of the speed of light. Now, the possibility that the Planck constant, 6.62606896 can be produced as of the multiplication of Planck energy and Planck mass requires critical analysis. This procedure breaks with the remaining nine constants as to how they are produced. In other words, one must critically consider not only whether this is a theoretically possible procedure for producing the Planck constant, but whether it is sound one. In my book, I treat this anomaly in detail. The second half of Table I contains the general theoretical Planck constants which do not reflect specifically measured matter-energy events. Only after having derived the specific numerical values of the measured matter-energy events represented in the first five Planck constants discussed above, is it possible to derive the next five general Planck constants. On the sixth row of Table I, the speed of light in vacuo is divided by the first radiation constant thus deriving the Planck energy constant, 1.956066112, previously listed on the second computational row of this same table. The Planck energy constant in then multiplied by the Planck mass, 3.487040766395, listed above on the first row of the table, thereby producing the Planck constant, 6.8208822743077. This value is quite distinct from the CODATA value for the Planck constant, 6.62606896. Yet, it is extremely close to Max Planck's original 6.885 value for the Planck constant forwarded by him in 1899. As explained in detail in my book, the CODATA Planck constant, 6.62606896, is erroneously based upon the multiplication of fractal numerical values grossly relating to ±1.956084456 and ±3.387040993, with any number of possible variations. The significant point is to recognize the devalued term, 3.387040993, which is similar but distinct from the 3.487040766395 Planck mass fractal value presented in Table I. In Table II one may observe how the general Planck constants are based upon and affected by the 3.387040993 value. The contradiction between the Planck mass value of 3.487040766395 as against the implied 3.387040993 value is brought out in Table II. My book presents an extensive critique of the theory behind the 6.62606896 fractal numerical value for the Planck constant; its empirical measurement is discussed indirectly. The seventh row for the generalized Planck constants involves Planck energy times Planck mass, obtaining the Planck constant, 6.8208822743077 fractal value and through standard procedure dividing it by the elementary charge. The numerical value for Planck constant in eV s, 4.257602516964, obtains. [The CODATA value for the Planck constant in eV s is 4.13566733.] On the eighth row, once more the same procedure obtains, multiplying Planck energy times Planck mass in order to obtain the Planck constant, 6.8208822743077, but this time it is divided by 2-pi, 6.283185307, thus deriving the reduced Planck constant, with a fractal value of 1.0855771302349. [The CODATA value for the reduced Planck constant is 1.054571628.] The ninth row of Table I divides the Planck constant by 2-pi obtaining the cited reduced Planck constant, 1.0855771302349 value, and then divides this fractal by the elementary charge, thus producing the reduced Planck constant in eV s, 6.775640131054. [The CODATA value for the reduced Planck constant in eV s is 6.58211899.] The final and tenth row of the table involves the reduced Planck constant divided by the elementary charge that yields the reduced Planck in eV s, 6.7756401302349, which in turn is divided by the reciprocal of the speed of light in order to obtain the reduced Planck constant in Me V fm. [The CODATA value for the reduced Planck constant in Me V fm is 1.97326963.] The computational procedure followed on the Earth/matriX Table of the Planck Constants Based on the Fundamental Physical Constants provides an analytical perspective devoid of any of the CODATA's questionable symbolic formulae. The analytical procedure on Table I relies totally upon equivalencies found within the numerical fractal values of the fundamental physical constants. There is no need to square the speed of light in vacuo or raise any of the terms to higher powers, nor is there a need to employ square roots. As shown on Table I, the ten cited Planck constants may be derived solely based upon basic math procedures involving the fractal numerical expressions of the Planck constants and selected fundamental physical constants. The results provided by the computational procedure followed on the cited table are derived theoretically from the implied numerical fractal values of the CODATA. Nonetheless, it is significant to note once more that the 6.8208822743077 numerical value derived for the Planck constant in this manner is close to the original 6.885 value forwarded by Max Planck in his 1899 lecture in Berlin. In my book I explore possible reasons why Max Planck may have changed the 6.885 value of 1899 to the 6.55 value in 1900 [the 6.55 value still listed in a Lange Handbook of Chemistry in 1944.]. Another significant point to note here, is that the ratio between the CODATA 6.62606896 value and Planck's 6.55 value is a fractal multiple near phi, ±1.618581731; imagine if the 6.626+ value were derived by multiplying the 6.55 figure times phi. Given the fact that Max Planck did not disclose his procedural computation to derive his constant, one may in fact imagine anything as an analytical possibility. In this case, however, the relational numerical values as illustrated in Table I suggest an analytical approach to the Planck constants and the fundamental physical constants beyond the traditional symbolic formulae presented by Max Planck or the CODATA international committee. By now, it has become apparent that the numerical value of the gravitational constant [G] is not present in the tables. By using the fundamental physical constants in order to derive all of the Planck constants without the gravity constant, G, is itself a most significant aspect of this analytical procedure. This obtains due to the presence of G in the original symbolic formulae forwarded by Max Planck, and its continued presence in the CODATA symbolic formulae. Further, every textbook and science writer whose work I have read about the Planck constants offer definition of these constants as of c, G, and h. From the analytical procedure followed in my book and on the tables presented here, the extent to which the fundamental physical constants intervene in the Planck constants is quite distinct from those traditional definitions. One can argue that G lies within some of the fundamental constants cited [as in the inverse fine structure constant], which is true. But, the fact remains that the numerical value of G [6.67428] does not appear directly by itself. Given the apparent theoretical contradiction and anomaly of the Planck constant value of 6.62606896, one can consider the nature of quantum physics at this point. Surely counter arguments may cite the measurements of the Planck constant that supposedly derive its empirical value and confirmation. The CODATA 6.62606896 fractal value is a mean obtained from experimental measurements through different methodologies. Yet, as is so often emphasized in quantum physics, one may query whether the fact that scientists seek to confirm the 6.62606896 number might actually produce that sought-after number through their experimental search as observers. By the stated rules of quantum mechanics today, one must consider the possibility that by seeking the practical confirmation of the theoretical value of 6.8208822743077 [ 6.82088 en bref ] for the Planck constant that they may possibly not only find it but produce it amongst their measured experiments. With the myriad of measured values for the Planck constant over its 110 year history, from 6.885, 6.55, 6.624, 6.6523, 6.626+, 6.62606896, etc., one can only wonder about the relationship between the existence of spacetime/motion events and their observation and measurement. It is not for me to say that the current scientific measurements that have produced similar fractal values around the 6.626-plus number for the Planck constant are incorrect; that is far beyond my practical experience. But, as determined in the Earth/matriX Table of the Planck Constants Based on the Fundamental Physical Constants, it is possible to say that a significant discrepancy exists between the CODATA value for the Planck constants and those derived in the manner as shown in this brief summation of my studies. I do suspect that Max Planck was initially correct with his 6.885 value, and that the 6.82088+ value derived herein is theoretically correct. Whether it is practically correct is another issue. It must be noted that these two values also reflect numerous constants in specific forms of matter-energy that involve a 1.36+ fractal numerical value. Consider doubling the 6.82088 value, which derives 1.364176. Similarly, the Max Planck original value of 6.885 doubles to 1.377 and is suggestive of the inverse fine structure constant. Consult the list of 1.36+ related physical and chemical constants on my web-site, www.earrthmatrix.com. An additional observation: when one compares the fractal numerical expressions of 6.626+ and 6.82088+ the fractal difference between them, 0.19488, appears to be enormous. But, when one is reminded that such a comparison is essentially at the sub-atomic particle level, then the difference may be perceived otherwise. Remember the numbers, not just the fractal expressions, as in the comparison:
Ultimately, there is nothing like looking at the numbers and seeing how they behave. One of the main problems touched upon in my research is the tendency in today's science writing to depend totally upon symbolic formulae and equations that supposedly represent numbers, but actually hide them and even disregard or confuse them in many cases. The Earth/matriX Table of Planck Constants Based on the Fundamental Physical Constants represents an effort to emphasize the numerical values of the constants and thereby propose a revision of the symbolic formulae which are at times not only misleading, but incorrect. With that purpose, I present this summation of my book entitled, Errors and Omissions in the CODATA and, The Planck Constants Based on the Fundamental Physical Constants [Earth/matriX Editions, 2010]. REFERENCES: Table I.-
Table II.-
...... ...... THE PLANCK CONSTANTS BASED ON THE FUNDAMENTAL PHYSICAL CONSTANTS AND ERRORS AND OMISSIONS OF THE CODATA The author derives the Planck constants as of the fundamental physical
constants, instead of as of the traditional symbolic formulae given in
the CODATA. The implied numerical values that are generally omitted in
the science literature and which serve as a basis for deriving the Planck
constants are identified in detail in their basic math. As of the analysis
of the implied Planck values, errors and omissions of the CODATA Planck
values are identified and treated extensively. The Planck constants are
reverse engineered in order to employ the fundamental physical constants
as their computational foundation. Various Earth/matriX Tables of the
Planck Constants Based on the Fundamental Physical Constants are presented
for the first time, illustrating how the fundamental physical constants
serve as the foundation to the Planck constants.
Purchase and download the complete e-book: Errors and Omissions in the CODATA and The Planck Constants Based on the Fundamental Physical Constants PDF file 142 Pages Earth/matriX Editions ISBN 1-58616-463-5 Price: $8.19US Introductory Offer
|
|
: |
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||
|
|
||||||||

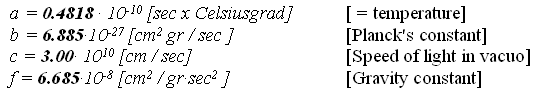
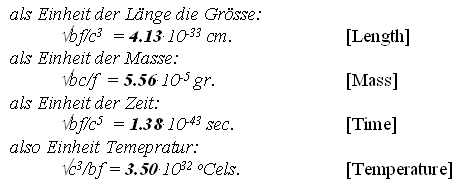


 New
Book
New
Book