E a r t h / m a t r i X
SCIENCE IN ANCIENT ARTWORK
AND
SCIENCE TODAY SERIES
Essay N°120
The Radian and the Anti-Radian:
A Method of Reckoning
by Charles William Johnson
Chapter III
Another historically significant number/fractal concerns the ancient Nineveh number 2268, and makes its appearance on the table of functions at the 13-degree mark. The actual function for 13 degrees is .226892803, which again represents a coincidence of numbers. We find two historically significant numbers related in this manner on the table. In other words, 13 degrees is .226892803 of the number of degrees in the radian. The pattern that is established on the table, then, concerns the multiple of this number for every 13 degrees within the 360-degree circle. It is stated that the ancients disliked fractions and preferred to work with whole numbers. This means that they knew the fractions and selected the whole numbers over the fractions. If, in this particular case, they employed the 2268 number/fractal instead of the .226892803 number, then the following pattern obtains.
| 13 26 39 52 65 78 91 104 117 | 2268 4536 6804 9072 11340 13608 15876 18144 20412 | 130 143 156 169 182 195 208 221 234 | 22680 24948 27216 29484 31752 34020 36288 38556 40824 | 247 260 273 286 299 312 325 338 351 364 | 43092 45360 47628 49896 52164 54432 56700 58968 61236 63504 |
One immediately notices the appearance of the 260c and the 364c on this particular pattern. The 364c day-count has been cited as representing the day-count used in computations within the ancient system. And, one cannot help but notice the relationship of numbers between the 260c and the 364c:
63504 - 45360 = 18144
Now, in regards to the 18c, another pattern is established as of the contemporary figure for pi, that is the 3.14159265 number/fractal.
| 18 36 54 72 90 108 126 144 162
180
360 378 |
.314159265 .628318531 .942477796 1.256637062 1.570796327 1.884955592 2.199114858 2.513274123 2.827433388
3.141592654
6.283185308 6.597344573 |
.1 .2 .3 .4 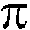 .5 .6 .7 .8 .9
2
2.1 |
In this case, the 260c fractal/number does not make its appearance on this series. However, on the 360c pattern, the 378c makes its appearance. One might further understand why the 18c day-count was chosen, given its direct expression in fractions of the concept of pi, as illustrated above in the column of numbers to the right of the functions.
From the perspective of computational math, then, one can imagine a system of reckoning whereby the 260c and the 364c are relational to one another as they both lie on the same 13c series. Whereas the 360c and the 378c series both lie on the 18c series, and would thereby be computationally relational. From the previous table alone, one may intuit the reason why the ancients selected the 360c for their calendar, both the ancient kemi as well as the ancient maya, given its obvious relationship to pi and the degrees in a circle.
The previous list obtains from dividing pi (3.141592654) into the numbers given for the functions on the table. That is in regards to the 18c. Now, let us divide the functions of the 13c by the number pi.

In the previous table, we find a most interesting and compelling example of a natural relationship between two ancient reckoning counts in Mesoamerica. The four legends concern the 676c, and the maya long count period refers to 1872000 days. In the previous example of 338 degrees, we can visualize a relationship of these counts: 676 (2 x 338), and the 1872 fractal/number resulting from the division of pi. Furthermore, we may observe the appearance of a maya-like series based on the maya long count fractal numbers (18, 36, 72, 144, 288, 576, 1152, 2304). And. although the 364c lies outside the confines of the 360-degree circle, we may observe once again how the 364c lies on the pattern of the 13c as previously noted.
Now, let us develop this series beyond the 360c circle, as though we were proceeding on to more revolutions around the circle. Let us see where this 13c takes us into more degrees on the second revolution around the circle.
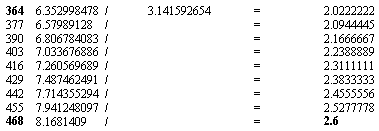
The significance of the 468 degree mark concerns the maya 1872000 long count period fractal (468, 936, 1872). And, now we see it in relation to the 260c (52c, 104c multiples).
Let us now do a little reverse engineering to consider the 2.304 maya alautun fractal number on the right hand column, and thereby see which degree would be in correspondence to it.
414.72 7.238229474 / 3.141592654 = 2.304
or,
| 2.304 1.152 .576 .288 .144 |
x | 3.141592654 = 7.238229474 x 57.29577951 = | 414.72 207.36 103.68 51.84 25.92 |
At first sight, the 414.72 number appears to be of no historical significance. However, if we double and halve the number, we thereby see it pertains to the natural number series of the 81c on which the 25920 Platonic cycle makes its appearance, as well as the historically significant kemi number 1296. (The natural series 2592 is discussed in Earth/matriX Essays 61 & 62.)
| .81 1.62 3.24 6.48 12.96 25.92 51.84 103.68 207.36 414.72 |
The manner in which patterns are established pertains to the numbers themselves and not to any arbitrary choice. For example, consider the 18c pattern. One might think that a pattern could begin before that number, say at the 6c. For one could think a series of 6, 12, 18, 24, 30, 36, 42, 48, etc. But, the ancients did not choose this particular series. They began the series based on the 18c. This obtains because the numbers 6 and 12 degrees produce unmanageable numbers. In fact, they are so unmanageable, they even appear to be related to other historically significant numbers that have been frowned upon throughout history.
| 6 | .104719755 / 3.14159265 | = | .03333333 |
| 12 | .20943951 / | = | .06666666 |
| 18 | .314159265 / | = | 1.0 |
In fact, with the 18c pattern/series of fractals/numbers, the very concept of one begins the series. At best, one might want to begin the series with the degree/unit 9, which yields the number .5, but again, as we mentioned, the beginning of the series is best served symbolically and functionally with the equivalency of the pi-like fractal and the unit one.
The maya-like series based on the 13c initiates with the fractal/number .72222222, as we have seen previously. Therefore, based on the table of functions for the radian, the 13c begins with the maya-like fractal/number 72c, and the 18c initiates the series with the fractal/number series based on the concept of pi. All other numbers of degrees before the 9c, 13c and 18c (degrees) on the table yield no obvious pattern that is related to the historically significant fractal numbers. As of the same procedure as above, their corresponding numbers are:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
= = = = = = = = = = = = = = = = = = |
.05555555 .01111111 .01666667 .02222222 .02777778 .03333333 .03888889 .04444444 .05 .05555555 .06111111 .06666667 .07222222 .07777778 .08333333 .08888889 .09444444 .1 |
***
Variations of Pi, the Radian and the Anti-Radian: Symbolism in Numbers
| Home | Books | Forum | Reviews | Links | Author |