E a r t h / m a t r i X
SCIENCE IN ANCIENT ARTWORK
AND
SCIENCE TODAY SERIES
Essay N°120
The Radian and the Anti-Radian:
A Method of Reckoning
by Charles William Johnson
Chapter IV
From the previous review, we have seen a relationship between the series of day/year counts, cycle counts and the natural numbers that correspond to the characteristics of a circle. We cannot repeat the table of functions for every possibility that exists in relation to a variation of the pi figure. But, we shall offer some selective information regarding different possibilities for pi for specific degrees. If any one number changes within the confines of the characteristics of the circle, then all the other numbers change in the relationships identified above. To repeat, let us review the numbers corresponding to pi as we know it today, 3.141592654, as given on most electronic calculators.
We have selected certain degrees/fractals for their historical significance in the different cases that follow. The 13c and 18c numbers are obvious. The 18.2 count represents the 364c pattern (182, 364); the 1872c refers to the maya 1872000 period; the 18.9c refers to the 378c (189, 378); and the 18.98 count represents the Mesoamerican calendar round of 18980 days. Remember, the numbers may be visualized as fractals, with a floating decimal, point since the functions shall vary in the same manner of number and places.
| 1° 13 18 18.2 18.72 18.9 18.98 |
.017453293 .2268928028 .3141592654 .3176499235 .3267256356 .3298672283 .3312634917 |
360° / 3.141592654 360 - 57.29577951 |
= = |
114.591559 (diametian) 57.29577951 (radian) 302.7042205 (anti-radian) |
By dividing the 360 degrees of a circle by today's value of pi, we see the length of the diameter/diametian (114.591559) appear, and by dividing that figure by two, we then see the radius/radian (57.29577951) make its appearance.
Now, with these same figures, if we were to construct a circle with a 260c (degrees/sectors) instead of the 360c normally associated with the circle, the following would obtain.
In this case, the 2.268 would represent the pi relationship for a 260c circle. In other words, 2.268 would be to the 260c circle as 3.1416 is to the 360c circle.
In the case of a 378-degree/sector circle, the 3.298 would represent the pi relationship. As the total number of degrees/sectors on a circle change, then the symbolic and proportional relationship of pi changes in number (though not in unit measurement). Interestingly enough, half of the 3.298672283 number, 1.649336142 is suggestive of the Sothic fractal number 1649457812 (3.298915624), which may signify a variant representation of pi.
| By reverse engineering, then, 1.649457812 | ||||
| 3.298915624 | x | 114.591559 | = | 378.0278844 756.0557687 |
We should remember, that I.E.S. Edwards, in The Pyramids of Egypt, (p.118), gave the measurement of the south base of the Great Pyramid of Giza as being 756.08 feet.
Now, let us suppose for a moment that the ancient reckoning system employed the 57.6 maya figure the radian. All of the previous numbers would change.
| 1 / 57.6 = .017361111 | ||||
| 1° 13 18 18.72 18.9 37.8 75.6 |
.017361111 .225694444 .3125 .325 .328125 .656249996 1.312499992 |
57.6 (radian) 115.2 (diametian) 360 / 3.125 (pi) |
= |
115.2 (diameter) |
Notice: 75.6 / 57.6 = 1.3125
The number/fractal for pi appears at the 18th degree. Therefore, if the ancients employed the reciprocal of seven number for pi, 3.142857142..., the other numbers would change in the following manner.
| 1° 13 18 18.2 18.72 18.9 18.98 |
.174603175 .2269841275 .3142857142 (pi like) .3177777785 .3268571436 .3300000008 .3313968262 |
360 / 3.142857142 = | 114.5454546 (diametian) 57.27272729 (radian) 302.727273 (anti-radian) |
Now, let us see what the numbers would look like if pi were tagged at 3.1416 as it often is presented today.
| 1° 13 18 18.2 18.72 18.9 18.98 |
.0174533333 .2268933333 .31416 (pi like) .3176506661 .3267263994 .3298679994 .33126426 |
360 / 3.1416 = | 114.5912911 (diametian) 57.29564553 (radian) 302.7043545 (anti-radian) |
Now, let us see when the 1728 natural number (27, 54, 108, 216, 432, 864, 1728) series is employed as the function for one degree.
| 1° 13 18 18.2 18.72 18.9 18.98 |
.01728 .22464 .31104 .314496 .3234816 .326592 .3279744 |
360 / 3.1104 = | 115.7407407 (diametian) 57.87037037 (radian) 302.1296296 (anti-radian) |
The fractal number 3.1104 is also found ancient Mesoamerica reckoning systems. A direct relationship is thus obtained among the different counts. Consider the following:
| maya fractal:18.72° | .3234816 / 3.1104 | = | 1.04 (maya count) |
| kemi fractal: 18.9° | .326592 / 3.1104 | = | 1.05 (kemi count) |
From the foregoing analysis, one may see how the fractal numbers may change regarding the characteristics of the circle and the table of functions in relation to some of the historically significant day/year and cycle counts. The variations are infinite. It is significant to note that the 13c series of numbers relates to the Nineveh fractal number 2268; and, the 18c relates directly to the expression of pi in relation to the 360c circle, given the fact they both lie on that same series of multiples.
It would appear as though the 260c and the 364c are related for carrying out computations together as they both lie on the 13c series of numbers. And, it would appear as though the 360c and the 378c are related in the same computational manner as they both lie on the 18c series of numbers.
The manner in which the different counts are computationally related may be witnessed in the following example.
| 10400 x 360 = 3744000 | / | 57.2957951 = 65345.10942 | / | 3.141592654 | = | 20799.99434 (20800) |
Further, in the maya long count (144, 288, 576...) the natural series, 1, 2, 4, 8, 16, 32, 64... is employed in relation to the long count fractal numbers. In ancient kemi, an historically significant count employed concerns the 21, 42, 84... series. Consider the following relation of the kemi (756c) and the maya (576c) in relation to the radian and pi, which is basically an indirect way of dividing by the number 18c:
| 756 / 57.2957951 | = | 13.19468915 / 3.141592654 | = | 4.2 | (756 / 18 = 42) |
| 576 / 57.2957951 | = | 10.05309649 / 3.141592654 | = | 3.2 | (576 / 18 = 32) |
By now we have noted that the ancient reckoning system fractal numbers are relational to the contemporary figures for pi and the radian. Throughout the Earth/matriX series, we have been exploring the relationships of the fractal numbers of the ancient reckoning system in relation to other historically significant numbers, without really relating them to contemporary mathematics. However, with the review of the characteristics of the circle, we have employed the contemporary figures and seen that the ancient numbers perform perfectly.
One conclusion that our analysis suggests is that the historically significant fractal numbers are themselves a product of the exact knowledge of the figures related to a precise apprehension of the measurements of pi and the radian. And, not only that, but they appear to have related all of that to the precise knowledge of the anti-radian.
The Maya Companion Numbers: 1366560 and 1385540
The maya companion numbers have been an intriguing source of analysis of the ancient reckoning system. First of all, it is difficult to accept the idea that the ancients thought in terms of millions of days or, much less in terms of the maya concept of the alautun, 23,040,000,000 days. Aside from this impressive concept of time, the companion numbers may be expressing relationships of the circle in terms of the anti-radian.
Consider the procedure for the 25.92 degree figure on the table of functions. Instead of dividing the degrees (fractal numbers) by the radian, let us divide them by the anti-radian (302.7042205):
| 25.92 / 302.7042205 | = | .085628142 / 3.141592654 | = | .027256284 .013628142 |
Given that the 25920 figure has been cited as a Precession number throughout history, let us do some reverse engineering and see what kind of number for the Precession the 1366560 figure would produce in the previous method of computation.
| .01366560 .0273312 x 3.141592654 |
= | .085863497 x 302.7042205 | = | 25.99124297 |
This figure is not bad for the concept of precession, generally cited as being between 25800 and 26000 years.
| .01385540 .0277108 x 3.141592654 |
= | .087056046 x 302.7042205 | = | 26.35223246 |
The maya are said to have employed the 25956 as a Precession figure.
| 25.956 / 302.7042205 | = | .08574707 / 3.141592654 | = | .02729414 .01364707 |
Again, one could review an infinite number of computations coming from the historically significant fractal numbers. Our concern for now is not to obtain the precise computation, but merely to explore the possibility that this could have been part of the method of computation itself. It is interesting to note that 1366560 - 1364707 = 1853, 3706. That is not a bad figure when we consider that the calendar round fractal number is 1898, 3796; a difference of 90 (another maya fractal number). And, furthermore, one could understand how a number obtained through the anti-radian procedure could be considering an accompanying number or companion number to the radian procedure.
To review:
| 25.92 | / | radian | = | .452389342 /
| = | .144 (maya long count fractal/number) |
| 12.96 6.48 3.24 | .72 .36 .18 |
| 25.92 | / | anti-radian | = | .085628142 / | = | .02725628 |
| 12.96 | .01362814 (maya companion-like fractal) |
The Aztec Calendar, for example, appears to reflect a design wherein the anti-radian is divided into half. This would mean that the computational procedure could be based on dividing the number of degrees to the circle by half of the anti-radian number, which would produce a maya companion fractal number related figure.
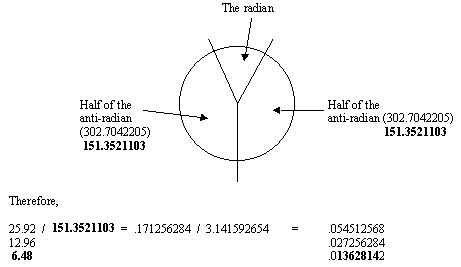
Now, the 151.3521103 number is suggestive of the historically significant maya number 151840, which is one ninth of the maya companion number 1366560.
| 25.92 | / | 151.840 | = | .170706006 / 3.1415951559 | = | .054337409 |
| 12.96 6.48 | .027168705 .013584352 |
| 1385540 - 1358435 | = | 27105 | ||||||||
| 13552.5 | - | 13665.6 | = | 113.1 | ||||||
| 226.2 | - | 226.8 | = | .6 |
If half of the anti-radian is 151.840, then the anti-radian is 303.68 (75.92 x 4).
| Consider, then: | 303.68 607.36 1214.72 2429.44 4858.88 9717.76 19435.52 |
This fractal number reminds us of the Nineveh fractal number 1959552:
In summary, then, one may visualize a table of conversions from one set of historically significant counts to another by way of the radian, the anti-radian and the concept of pi. And, as we mentioned earlier, the precision of pi and the radian (and the anti-radian) are based on the contemporary knowledge about the figure of pi (3.141592654).
| 6.48 | / | 57.2957951 (radian) | = | .11309705 / |
= | .035999909 (.0360) |
| 6.48 | / | 151.3521103 (½ anti-radian) | = | .042814071 / |
= | .013628142 |
In this manner, we see how the conversion from a kemi fractal/number (1296, 2592) to a maya long count (360c) and a maya companion-like number (1363814c) are achieved through the radian and the anti-radian in relation to the concept of pi. Adjustments could be made to achieve any precise fractal number required on either side of the conversion.
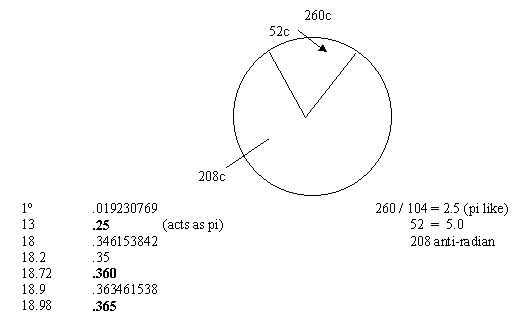
Aside from a strict computational representation with the circle and the historically significant day/year counts, one might imagine a symbolic representation of the counts on the circle. For example, let us see what the data regarding the 360c circle would look like if we considered the radian to be represented in a symbolic manner by the 52c.
| 1 / 52 = .019230769 |
||||
| 1° 13 18 18.2 18.72 18.9 18.98 |
.019230769 .249999997 (.25) .346153846 (acts as pi) .35 .360 .363461538 .365 |
360 / 104.0 52 308.0 |
= = = |
3.461538462 6.923076923 anti-radian |
Notice in this case, how the numbers correspond to the representation in the ancient reckoning system. The calendar round of Mesoamerica consists of 18980 days (52 x 365), as shown in a fractal variation above. And, the maya long count period of 1872000 (5200 x 360) days corresponds to the 360c as illustrated also above in a fractal expression.
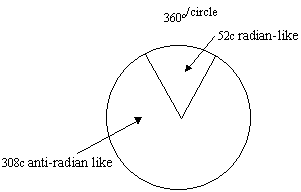
In this case, the Aztec calendar could easily follow such a method of computations, whereby the degrees of the circle and its internal coordinate elements could reflect the day/year counts. We have presented examples of such representations in numbers/fractals in Earth/matriX Essay No.88.
The 378c circle reflects a distinct symbolic representation.
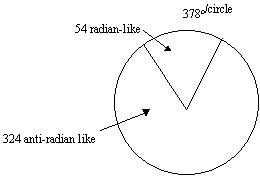

If a symbolic representation were made on a 378 degree circle in this manner, the the pattern would evolve:
| radian | anti-radian |
| 54 108 216 432 (Consecration) |
324 648 1296 2592 (Platonic Cycle fractal) |
Now, consider the following.
432 + 2592 = 3024
In other words, the radian plus the anti-radian of a 378 degree symbolic circle would equal the anti-radian of a symbolic 360 degree circle.
| 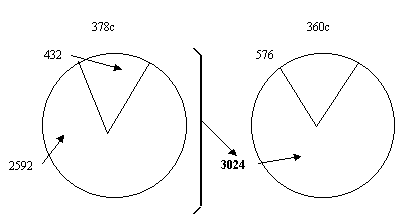 |
The numbers/fractals are such in relation to the 360c and 378c circles, that the radian plus anti-radian of this particular 378c circle equals the anti-radian of the 360c circle.
With regard to the 260c circle a similar pattern evolves as that of the 360c circle, although the pi-like concept has now changed position.
The 364c circle requires further comment. However, due to its complex nature in terms of symbolic representation, we consider that another essay should be dedicated to its explanation. Its analysis involves apparently complex fractions which would require a space equal or longer than this entire essay. For now, with the previous analysis of the different symbolic circles, we should at least have an idea how to relate the natural numbers of a circle and those coming out of the ancient reckoning system.
Observations
The day/year and cycle counts from the ancient reckoning system perform exactly as of the contemporary numbers; something that most scholars would not think possible. To have the different counts perform among themselves exactly by way of these precise numbers might be thought to represent another case of coincidence. However, we prefer to think that the ancient counts were chosen based upon a precise knowledge of the circle.
We have seen how the historically significant fractal numbers just happen to correspond to precise patterns within the contemporary numbers of circles. For the ancients to have chosen such precise numbers based on some other criterion would surely be a case of a mathematical miracle, given the odds against such a coincidental such. It is difficult to think that the ancients purely out of chance chose: the 13c (of Mesoamerica) in relation to the 2268c (of Nineveh); the 18c (of the ancient maya and kemi); in relation to today's figure of pi, the radian and the anti-radian; as well as, all the other historically significant fractal numbers discussed here. The probability of something like that happening out of chance seems to be outside the realm of mathematics itself; no number could reach that high.
To review, many of the fractal numbers that are natural to a circle reflect relationships of historically significant counts.
The 13c (maya) arises in relation to the 2268c (Nineveh). Every thirteen degrees of a circle the radian increases by approximately .2268c. Within that pattern, one may find historically significant fractal numbers on the series: 13c, 26c, 39c, 52c, 65c, 78c, 91c, 104c, 117c, 130c, 182c, 208c, 234c, 260c, 312c, 325c, 338c, 351c, as well as the 364c on the second revolution around the circle. Within the radian pattern of that series, one may find other historically significant counts, such as, the 2268c, the 4536c, 6804c (3402), 9072c, 11340c, 18144c, 22680c, 34020c, 36288c, 54432c, and the 56700c.
The 18c (maya and kemi) lies in relation to the progression of multiples of pi. Every eighteen degrees on a circle the radian increases by one-tenth of pi. Within that pattern, one may find historically significant fractal numbers: 18c, 36c, 54c, 72c, 90c, 108c, 144c, 180c, 216c, 236c (Dresden), 252c, 270c, 288c, 324c, 360c, and even the 378c on the second revolution around the circle.
The radian (57.2957951) is suggestive of the 57.6c (maya) and performs easily in relation to the 75.6c (kemi).
The anti-radian (302.7042205) is suggestive of the 302.4c (kemi) and performs exactly thereof.
The 330c (degrees/units) relates by way of the radian to the 5.76c (maya).
The 325c (degrees/units) relates by way of the radian to the 5.67c (kemi)
The 260c relates by way of the radian to the 4.536c (Nineveh).
The maya long count 144c (degrees/units) relates by way of the radian to the 216c (216, 432, 864).
The 216c (degrees/units) is suggestive of the 3.796c calendar round (Mesoamerica).
It is quite impossible to review all of the relational possibilities between the historically significant counts (fractal numbers) and the natural numbers and fractals arising out of the mathematical and geometric treatment of the circle. We have examined only a few of the main ones, which should serve as a basis for considering other relationships in the future.
By way of the radian, the anti-radian and the concept of pi, in the exact terms of today's figures, one can convert effortlessly from one historical count to another in many cases. One is tempted to suggest that the ancients did it in the precise manner in which we have illustrated above. However, this cannot be stated. There is no historical evidence to support such a statement. Only some isolated numbers exist in the historical record. And, the historical record is all but silent on how the ancients performed their computations.
We have examined a few ways in which the historically significant fractal numbers are suggestive of methods of computation in relation to the natural numbers coming out of the mathematical and geometric treatment of the circle. This is not to say that the ancients did it in this way. We highly suspect that a similar procedure may have been involved. But, until we find the notebooks of the ancients who actually performed these computations, any analysis of the logic of numbers shall remain pure speculation.
That does not mean, however, that the way in which we have achieved the conversions is useless. For even though we may not be able to achieve the link between this particular method and approach with the ancient's method of reckoning, the procedure examined in this essay represents a valid method for analyzing the behavior of a circle and its elements.
One thing that may be learned from all this speculation, is that we should consider the treatment of the circle in its entirety: pi, the radian and the anti-radian.
***
Your comments and suggestions are greatly appreciated:
e-mail: johnson@earthmatrix.com
RESEARCH IN SCIENCE ARTS/ECOLOGY
Science in Ancient Artwork Series Essay No.120
The Radian and the Anti-Radian: A Method of Reckoning
New Orleans, Louisiana
28 April 1999
;USA
Reproduction prohibited without written consent of the author.
| Home | Books | Forum | Reviews | Links | Author |