
The Square Root of Ten
(3.16227766)
and
Its Reciprocal
(.316227766)
Charles William Johnson
In ancient reckoning, the method of duplatio/mediatio (doubling/halving) numbers appears to have been quite prevalent in the computations. As we have discussed frequently in the Earth/matriX essays, a number series based on doubling shall yield the powers of numbers as well. In this regard, the ancient procedure of doubling/halving numbers may have represented a simple method for computations, which are viewed as being more complex today. Furthermore, we have often emphasized the possibility that the ancient reckoning system may have also employed the method of tripling numbers and hence dividing them by three as well. With that, any number becomes available within the system.
The square root of ten (3.16227766) from the perspective of ancient reckoning, along with its based numbers, 2 and 5 (2 x 5 = 10), become quite significant.
|
|
1 / 3.16227766 = .316227766 |
In a system of doubling and halving numbers, the numbers two and five are significant regarding multiplication and division:
| 756 / 5 = 151.2 |
756 x 2 = 1512
|
And, given the fact that the ancients disliked fractions, we may then comprehend the idea of a floating decimal place, which would nullify the decimal point (fractional expression) in favor of a fractal one: 1512 : 151.2. One cannot help but ponder the possibility of the 52c calendar round of Meso-America as representing some kind of symbolic significance for this mathematical expression (5 or 2 as multiplication or division).
From the perspective of math and geometry, the square roots of numbers within the series also becomes relevant. In fact, in such examples as that of the Great Pyramid, as we shall observe below, the square root of the number two (![]() 2) becomes all-important. One may even wonder whether the number 707c, which has been cited as an historically significant number may have come from the square root of two. Further, we shall consider the squares roots of the numbers five (
2) becomes all-important. One may even wonder whether the number 707c, which has been cited as an historically significant number may have come from the square root of two. Further, we shall consider the squares roots of the numbers five (![]() 5) and ten (
5) and ten (![]() 10).
10).
|
|
|
|
|
|
One must remember that the square root of five has also been employed to develop the Golden Section:
|
|
= | 1.618033989 |
| 1 / 1.618033989 = .618033989 |
Square Roots and Reciprocals
The square root of the number two appears in many different places within the ancient reckoning system. We shall discuss only a couple of these aspects significant to our own research.
Within the doubling/halving series of numbers, such as in the Maya Long-Count numbers, the square root of two plays a significant role.
The Maya long-count numbers and categories are cited as:
| 23040000000 | alautun |
| 1152000000 | kinchiltun |
| 57600000 | calbatun |
| 2880000 | pictun |
| 144000 | baktun |
| 7200 | katun |
| 360 | tun |
From one level to the other, the multiplication by two is obvious on the previous long-count series (plus, the addition of one zero). For now, let us simply consider the fractal expressions of these numbers.
|
36 x 2
|
= 72 |
|
72 x 2
|
= 144 |
|
144 x 2
|
= 288 |
|
288 x 2
|
= 576 |
|
576 x 2
|
= 1152 |
|
1152 x 2
|
= 2304 |
The square root of two comes into play regarding the level of roots among these long-count fractals.
|
24 x
|
||
|
33.94112552 = 1152 (kinchiltun fractal)
|
||
Let us offer another example for clarity of method:
| 33.9411255 x |
||
| 482 = 2304 (alautun) |
One may wonder whether the ancients comprehended such an elementary relationship among the series of numbers based on the doubling/halving method. Consider the following relationship discerned from other ancient reckoning numbers. The Great Pyramid's baseline measurement is often cited as 756 feet (189, 378, 756, 1512).
|
|
It is significant to observe how another historically significant number from ancient China and Meso-America makes its appearance in these fractal computations of square roots.
1944, 3888, 7776
Were we to consider the possibility that 3888 were to have been employed in the base measurement of the Great Pyramid, then, the following would obtain. If there had been a correspondence between the historically significant 3888 count and the baseline of the Great Pyramid, we would have the following for the measurement of the latter:
38.882 = 1511.6544 / 2 = 755.8273 feet for the base of the Great Pyramid.
The ![]() 2 would also become significant in this sense for the diagonal measurement of the base of Great Pyramid of Giza. If the side measurements of the Great Pyramid are 755.8273 feet square, then the diagonal measurement from corner to corner of the Great Pyramid would be:
2 would also become significant in this sense for the diagonal measurement of the base of Great Pyramid of Giza. If the side measurements of the Great Pyramid are 755.8273 feet square, then the diagonal measurement from corner to corner of the Great Pyramid would be:
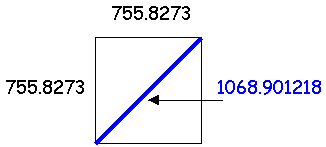
Just how significant might these computations be, may be viewed when we consider this particular measurement (1068.901218) in relation to the ancient Meso-American count of 676c years.
| 1068.901218 x |
=
|
3380.162443 |
| 6760.324885 |
The square root of two suggests perfect geometry and math:
|
|
||
|
1 / 1.414213562
|
=
|
.707106781
|
|
.707106781
|
:
|
1.414213562
|
|
1.414213562 / 2
|
=
|
.707106781
|
|
1 / 1.4142136237
|
=
|
1.41421356237 / 2 |
In other words, the reciprocal is simply half its own value; meaning that its reciprocal may obtained by its being divided by two.
So occurs the same feature for the reciprocal of five and ten:
|
1 /
|
||
|
2.236067978
|
:
|
.447213596 fractal
|
|
2.236067978 x 2
|
=
|
4.472135955 |
|
1 / 2.236067978
|
=
|
.447213596 x 5 |
The most intriguing aspect of the square root of ten is the fact that its reciprocal is fractally the same number.
|
|
||
|
1 / 3.16227766
|
=
|
.316227766
|
|
3.16227766
|
:
|
.316227766 |
|
1 / 3.16227766
|
=
|
.316227766 x 10 |
The square root of ten reveals the same terms, albeit a different floating, decimal place, on either side of the equation. Aside from the debated and intriguing possibility of ![]() 1 = 1 / 1 = 1
1 = 1 / 1 = 1
the ![]() 10 (3.16227766) is probably the most intriguing number, given the fact that it always renders results in the same fractal expression, for the same terms with different signs:
10 (3.16227766) is probably the most intriguing number, given the fact that it always renders results in the same fractal expression, for the same terms with different signs:
756 x 3.16227766 = 2390.681911
756 / 3.16227766 = 239.0681911
where only the decimal places changes.
Turning our attention back to the square root of two, we see how it suggests many computations of ancient reckoning, and even with today's physical constants.
|
365c day-count /
|
=
|
258.093975133
|
(Precession today, 25800c) |
|
260c day-count /
|
=
|
183.847763108
|
(neutron:electron mass ratio: 1838.683662 |
|
2880 /
|
=
|
2036.46753
|
(remember the Dresden Codex, 236c) |
|
4072.93506
|
|||
|
8145.870119
|
|||
|
doubles to
|
|||
|
1.36665025511
|
[recall maya 1366560c] | ||
|
2036.46753 also doubles to 16291.74024
|
|||
In other words, 1152 x ![]() 2 = 1629.174024, and
2 = 1629.174024, and
if 1629.174024 minus Sothic 1649.457812 then equals 20.283788
This term is suggestive of Meso-American 2028c Four Suns Legend number and again, that of ancient kemi 378c. We may recall that the projected height for the Great Pyramid is generally 481.5 feet. Consider the following relationships between the Legend of the Four Suns number, 2028c and the projected height of the Great Pyramid:
| 1 / 481.5 = | .002076843 |
| .001038422 | |
| .00051211 | |
| .000259605 | |
| ... | |
| .000002028 |
The encoded relationships are many. Consider the Nineveh number, 1959552c fractal expression.
| 1 / .000002028 | = | 493046 | ||
| 986112 | ||||
| 1972224 minus 1959552 | = | 12672 | ||
| 6336 | ||||
| 3168c |
At every step of the way, we find historically significant numbers (2028c, 1959552c, 3168c) in relation to one another in elementary computations of remainder math.
Even Planck's constant 6.6260755 (today's physical constant figure/fractal) suggests the ancient Maya period 1872000 (half being 936c).
6.6260755 x ![]() 2 = 9.370685837 [936c]
2 = 9.370685837 [936c]
A strange computation appears in this regard. What if we employ the 936c in reverse engineering: 936000 / ![]() 2 661851.9472 minus 662607.55 (Planck's fractal), then, we obtain as the difference 755.6028093, which is suggestive of the baseline of the Great Pyramid.
2 661851.9472 minus 662607.55 (Planck's fractal), then, we obtain as the difference 755.6028093, which is suggestive of the baseline of the Great Pyramid.
In relation, then, to all of the computations shown for the square root of two, we must remember that the square root of five could be employed, thereby obtaining the same results simply by changing the sign of the computation from division to multiplication or vice versa. And, one must also remember that the square root of three would offer similar computations, given the fact that the method of trebling and dividing by three seems to have also been followed by the ancients.
|
1 / 1.732050808
|
=
|
.577350269 |
|
1.732050808 / 3
|
=
|
.577350269 |
|
1.732050808
|
=
|
.577350269 |
|
1 / 1.732050808
|
=
|
.577350269 x 3 |
Even the reciprocal of seven, as we have reviewed in other essays, plays a significant role in the ancient computations.
|
|
||
|
/ 2.645751311
|
= |
.377964473
|
|
.755928946
|
Conceivably, then, the 755.928946 could represent a computational variation for the baseline measurement of the Great Pyramid. If one were to divide the base of the Great Pyramid into eight halves along the four sides, then one would have 8/7ths at .377964473 or, a perimeter for the Great Pyramid of fractal 3023.715784 feet.
8 / 7 = 1.142857142 x 360 degrees = 411.4285714 fractal
4.114285714 - 1.414213562 = 2.700072152 fractal
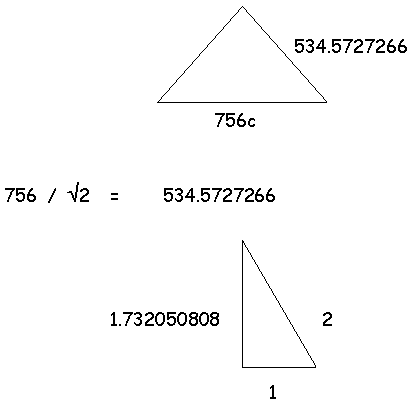
22 - 12 = ![]() 3 (1.732050808)
3 (1.732050808)
One may wonder whether the general computations in math and geometry simply reflect the measurements of the Great Pyramid. Consider the square root of two:
| 1.14213562 | |||
| 2.828427125 | |||
| 5.656854249 | |||
| doubles to | |||
| 189812531.2 | [calendar round 18980c] | ||
| ... | |||
| 106854955623 / |
755.5786373 fractal | ||
| 755.43 feet North wall -GP | |||
| 755.77 feet West wall -GP | |||
|
1 /
|
1068.549556 = .000935848 [maya 936c] | ||
|
1 /
|
1872000 = .0000005341880342 | ||
|
1068376068 [fractal representing the diagonal of the Great Pyramid]
|
|||
Further, as we shall examine more closely in a later essay, there appears to be a direct relationship between the Meso-American count of 676c and the measurement of the Great Pyramid by way of the square root of five
338c x ![]() 5 = 755.7909764
5 = 755.7909764
One may suggest that there is a direct relationship between the Maya long period (1872000c) and the diagonal measurement of the Great Pyramid.
The square roots of two and three approach a pi-like number:
![]() 2 +
2 + ![]() 3 = 3.14626437 pi-like figure
3 = 3.14626437 pi-like figure
![]() 2 +
2 +![]() 5 = 3.65028154 [day-count figure 365.2422]
5 = 3.65028154 [day-count figure 365.2422]
But, the square root of ten reflects something beyond the computational dreams of the ancient reckoning system. We have seen how this particular number may relate to historically significant numbers of the Great Pyramid. Now, look at the reciprocal of ten:
|
=
|
3.16227766 | |
|
1 /
|
3.16227766 = .316227766 |
Still more intriguing is the series of the square root of ten to the power of three:
| 3.16227763 |
=
|
31.6227766 |
| 31.62277663 |
=
|
31622.7766 |
| 31622.77663 |
=
|
3.1622776613 |
| etc. |
Or, consider different powers:
| 3.162277664 | = |
100 |
| 3.162277665 | = |
316.227766 |
| 3.162277666 | = |
1000 |
| 3.162277667 | = |
3162.227766 |
| 3.162277668 | = |
10000 |
| 3.162277669 | = |
31622.7766 |
| 3.1622776610 | = |
100000 |
| etc. |
Notice how suggestive the square root of ten is to the ancient reckoning maya companion number (1366560).
3.16227766 x 6 = 18.9736659609
Let us take once again the commonly cited measurement for the baseline of the Great Pyramid:
| 7563 | = | 432081216 | ||
| 432081216 / |
=
|
136636077.7 |
Maya companion number: 1366560.
Reverse engineering would reveal the following computation:
|
756.03674133
|
= | 432144216 / |
= | 136656000 |
|
1512.073483
|
||||
|
3024.146965
|
Therefore, in relation to the historically significant numbers and their fractal expressions, we may have the following computation:
338 x ![]() 10 = 1068.849849 [Meso-American 338, 676c]
10 = 1068.849849 [Meso-American 338, 676c]
Or, we take the side measurement of the Great Pyramid:
755.7909764 x ![]() 2 = 1068.849849
2 = 1068.849849
The ancients may have been communicating the mathematical and geometrical symbolism of the square roots and their reciprocals in their artwork. Take for instance the following computation:
|
3.16227766 (
|
=
|
1.00658442 |
| 2.013168484 | ||
| 4.026336968 | ||
| ...doubles to | ||
| 16491.86722 | ||
|
1649.187622 minus Sothic 1649.457812
|
=
|
.27018976 |
| .13509488 |
Observations
The square roots and their reciprocals of certain number would appear to be related directly to the measurements and their fractal expression of specific ancient reckoning counts. As we have seen above, some of the more commonly known day-counts relate directly to the measurements of the Great Pyramid.
The square roots and their corresponding reciprocals of the number 2, 5, and 10 appear to relate easily to the series of numbers within the ancient reckoning system. Further, other numbers, such as the square root and reciprocal of seven also occupy a prominent place within the ancient reckoning system as we have seen here and in other essays within the Earth/matiX series of essays.
The square root of ten (3.16227766) and its reciprocal (.316227766) appear to occupy a special place within the ancient computations. From such a procedure, one would expect that the ancient reckoning system would recognize, and possibly, be based upon the concept of fractal expressions and the floating decimal place. A study of the square root of ten and its reciprocal would easily teach a student such a possibility in reckoning numbers.
©2001-2013 Copyrighted by Charles William Johnson.
All rights reserved. Reproduction prohibited.
email : johnson@earthmatrix.com
and Its Reciprocal (.316227766)
ISBN 1-58616-313-2
Earth/matriX:
Science in Ancient Artwork
| Home | Books | Author | All Essays |