Charles William Johnson

Before considering the Beal Conjecture below, we should make a few remarks about Fermat's Last Theorem or conjecture, since both of these conjectures are related. With regard to Fermat's Last Theorem, the last-digit terminations determine the possibility of solutions for that theorem. The stipulations of the equation cited by Fermat refer to computations on a vertical plane for each particular power (greater than two) of the natural numbers.

x ⁿ + y ⁿ = z ⁿ

The relation of equivalency concerns whole integers for the terms and exponents greater than two (2).

There are no solutions to this equation as recently purported by Andrew Wiles and other mathematicians in their study of elliptic curves and modular forms.

However, there appears to be an easier method for obtaining a clear proof of this equation and the absence of any relations of equivalency as we have illustrated in different essays and extracts in the Earth/matriX series (Cfr., Earth/matriX, Extract 38, 1999). One need only review the exponents of n3, n4, n5, and n6 for the first ten natural numbers in order to determine the fact that there are no solutions for this theorem. The reason for this, is that the first ten numbers in relation to the exponents of n3, n4, n5, and n6 produce a repeat pattern of last-digit terminations for all natural numbers (1 to infinity) and for all exponents (1 to infinity). Therefore, what holds true for the first ten numbers, holds true for all numbers given the existence of the four patterns of the last-digit terminations and the rules of simple addition.

In other essays and extracts, we have offered many examples of this proof. However, we shall list a few examples here, merely to offer an illustration of the patterns and their behavior according to the terms of Fermat's Last Theorem. For a more detailed analysis, one should refer to the various essays and extracts posted in the Earth/matriX series.

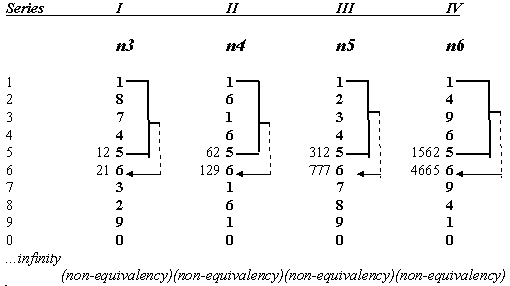
From the previous table, one may observe how it becomes impossible, in adding numbers that end in a one (1) and a five (5), to obtain a third product that ends in a six on the progression of natural numbers and their exponents.

The Beal Conjecture represents a similar proposition, whose limiting conditions makes it impossible to find a solution or relation of equivalency for the terms of the equation. As stated, with regard to the Beal Conjecture,

©1999-2015 Copyrighted by Charles William Johnson. All rights reserved. reproduction prohibited.

THE GOLDBACH CONJECTURE AND THE UNIVERSE OF PRIMES

Book: THE GOLDBACH CONJECTURE AND THE UNIVERSE OF PRIMES The Goldbach Conjecture and the Universe of Primes examines the even-sum tables of the natural numbers and prime numbers in proving the conjecture. The explanation of the inner workings of the Goldbach conjecture are rendered into simple math. Knowing how to add is all that is required. Profusely illustrated with easy-to-read math tables explaining how the sum of primes perform in relation to the conjecture. The author examines the Goldbach Conjecture, a 262 year-old conjecture. It is impossible to prove the Goldbach Conjecture in the manner in which the theorists of mathematics have been demanding. Instead of a resolution based on algebra, an explanation of the Goldbach Conjecture based on the numbers is required. In fact, this may be a simpler task than imagined until now. Purchase and download this Earth/matriX eBook The Goldbach Conjecture and the Universe of Primes Author: Charles William Johnson Price $8.64 US

 

Link: The Beal Conjecture: Submission Number Two