|
Earth/matriX The Integer (20) Calendar Reckoning
and
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table of Contents The
Integer (20) Calendar Reckoning and
|
THE INTEGER (20) CALENDAR RECKONING AND
ASTRONOMICAL TABLES: ANCIENT MEXICO
by
Charles William Johnson
Part I
The 360 Day-Count
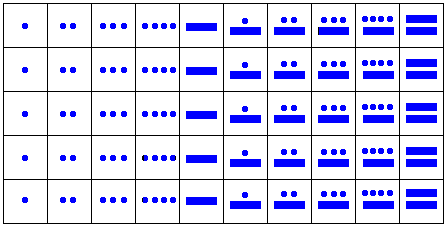
The numbering system of mayas consisted of three symbols: a shell-shaped
figure that represented zero (![]() );
a dot or point for the number 1 (
);
a dot or point for the number 1 (![]() ); and, a straight bar figure represented the number 5 (
); and, a straight bar figure represented the number 5 ( ![]() ). These symbols were arranged vertically at distinct positional levels.
). These symbols were arranged vertically at distinct positional levels.
The positional levels determined specific values, whereby the given number at a particular level would be multiplied by that level's corresponding constant value. The following is generally cited as the basis of the system, although now it is known that there were more than five positional levels.
| 23,040,000,000 | days | = | alautun |
| 1,152,000,000 | " | = | kinchiltun |
|---|---|---|---|
| 57,600,000 | " | = | calbatun |
| 2,880,000 | " | = | pictun |
| 144,000 | " | = | baktun |
| 7,200 | " | = | katun |
| 360 | " | = | tun |
| 20 | " | = | uinal |
| 1 | " | = | kin |
The maya system of the long count counted time-cycles in such a manner, that 20 kins (days) equaled 1 uinal (1 month); 20 uinals equal 1 tun (a year); and successively in this manner of multiples of twenty. We obviously have no commonday words in our language for an alautun, a time-cycle of 23,040,000,000 days, other than stating that that is a long time, over 63 million years.
For example, the number 1 (![]() ),
in column one would have a distinct value depending upon its placement
at each of the five levels. At positional level:
),
in column one would have a distinct value depending upon its placement
at each of the five levels. At positional level:
| V | = | 44,000 | (or 400 years); |
| IV | = | 7,200 | (or 20 years); |
| III | = | 360 | (or 1 year); |
| II | = | 20 | (one month); |
| I | = | 1 | (or one day); |
Such would be the translation of the constants into a specific number of years, given that 360 was the calendar count involved (360 days = 1 year, plus 5 extra days of the uayeb).
Similarly, regarding the number 5 (![]() ),
the values would change as the number five would now be multiplied by
the constants. Then, the number 5 would represent at positional level:
),
the values would change as the number five would now be multiplied by
the constants. Then, the number 5 would represent at positional level:
| V | = | 720,000 | (or 5 times 144,000 days; 5 baktuns); |
| IV | = | 36,000 | (or 5 times 7,200 days; 5 katuns); |
| III | = | 1,800 | (or 5 times 360 days; 5 tuns); |
| II | = | 100 | (or 5 uinals; 5 times 20 days); and, |
| I | = | 5 | (5 times 1 day; 5 kins). |
The maya long count, then, would be the cumulative sum of values generated in a specific column of figures. Let us examine a particular number example; the number 36,108 would be expressed in the following manner:
| = | 5 times | 7,200 | = | 36,000 | |
| = | 0 times | 360 | = | 0 | |
| = | 5 times | 20 | = | 100 | |
| = | 8 times | 1 | = | 8 | |
| 36,108 | |||||
The creative nature of the maya numbering system becomes obvious at once. In fact, a similar counting system was used by other peoples of ancient Mexico (the mexicas and aztecs), while some authors consider that the original counting system was developed by the olmec culture.
Without entering into a discussion of who-did-what-first, one is concerned with the procedure of such extensive calculations with numbers running into the millions on the fifth positional level and beyond. For even though the ancient peoples of Mexico might have been able to visually represent the numerical result of 18 times 144,000 (i.e., 2,592,000), it becomes intriguing to enquire how they actually effected the multiplications. With that concern in mind, we have attempted to understand how these calculations and reckonings may have been achieved without the need for multiplication.
The enquiry began with the numbers 1 through 20 and the corresponding values for each positional level. The search has the purpose of understanding why those particular constant values were chosen as cut-off points on those levels.
The integer 360 is obtained by multiplying 18 x 20, which in calendaric terms represents 18 months of 20 days. The older calendar reckoning was based on 13 months of 20 days and yielded a day-count of 260. But, we shall first examine the 360 count, since that pertains to the values cited in the tun figure.
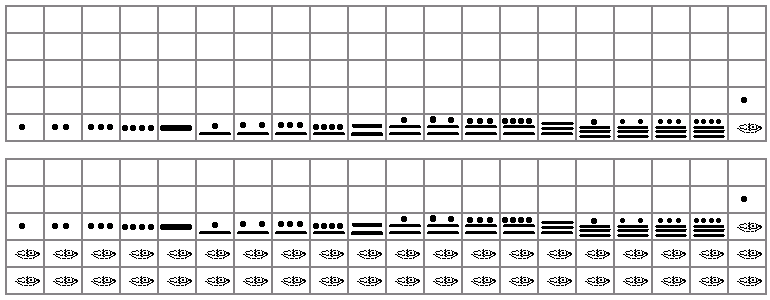
The following Table of Numbers is then implied in the procedure of multiplying the numbers 1-20 with each one of the five positional level's constants:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
By carrying through this multiplication procedure with every combination cited, the following Table of Numbers obtains:
| 144,000 | 288,000 | 432,000 | 576,000 | 720,000 |
| 7,200 | 14,400 | 21,600 | 28,800 | 36,000 |
| 360 | 720 | 1,080 | 1,440 | 1,800 |
| 20 | 40 | 60 | 80 | 100 |
| 1 | 2 | 3 | 4 | 5 |
| 864,000 | 1,008,000 | 1,152,000 | 1,296,000 | 1,440,000 |
| 43,200 | 50,400 | 57,600 | 64,800 | 72,000 |
| 2,160 | 2,520 | 2,880 | 3,240 | 3,600 |
| 120 | 140 | 160 | 180 | 200 |
| 6 | 7 | 8 | 9 | 10 |
| 1,584,000 | 1,728,000 | 1,872,000 | 2,016,000 | 2,160,000 |
| 79,200 | 86,400 | 93,600 | 100,800 | 108,000 |
| 3,960 | 4,320 | 4,680 | 5,040 | 5,400 |
| 220 | 240 | 260 | 280 | 300 |
| 11 | 12 | 13 | 14 | 15 |
| 2,304,000 | 2,448,000 | 2,592,000 | 2,736,000 | 2,880,000 |
| 115,200 | 122,400 | 129,600 | 136,800 | 144,000 |
| 5,760 | 6,120 | 6,480 | 6,840 | 7,200 |
| 320 | 340 | 360 | 380 | 400 |
| 16 | 17 | 18 | 19 | 20 |
This Table of Numbers (360c) reveals many significant aspects which we shall now examine in detail. The positional level I involves the unit-numbers 1 through 20. We did carry out the positional level II multiplication to the 40th place, but proved to be unnecessary as numbers began to repeat themselves. Given that the number 20 is the significant integer of the system, carrying the calculation out to the 20th place is sufficient to comprehend the system.
The values of positional level I are 20 times less than those of level II; level II is 18 times less than level III; the values of level III are 20 times less than those of level IV; and, the values of level IV are 20 times less than those of positional level V. Hence, another way of expressing this is: level V is 144,000 times greater than level I, the values of level IV are 7,200 times greater than the values of level I; etc. In all cases, the different levels represent multiples of 20.
One should notice the placement of the zeros at each particular level, for this shall be meaningful in the remainder of the analysis regarding methods of calculations. For example, positional level V shows values with at least three zeros ending their terms; level IV with at least two zeros; and levels III and II with at least one zero at the end of each value.
The most significant aspect of the Table of Numbers is the cut-off point 360 at the positional level II, 18. This integer then becomes situated at positional level III, 1. The number 360, as mentioned, is the product of 18 x 20, which involves the relation months/days.
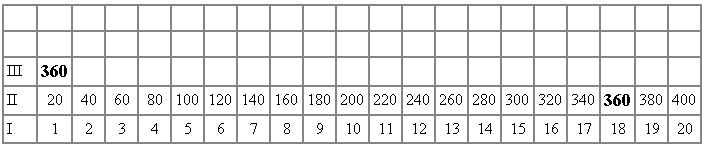
The relationship concerns the calendar count of 360 based on time-cycles.
Positional level III ends at the 20th integer with the value of 7,200, which begins also positional IV. It should be no surprise that positional level IV ends with the values of 144,000, the same constant that initiates positional level V.
The Table of Numbers, then, appears to arbitrarily be set at 360, since according to the logic of the integer 20, positional level III should begin with the number 400. However, the Table of Numbers reflects the logic of calendar reckoning, which in this case utilizes the earth's approximate time-cycle in seasonal years as a means for programming the entire set of values listed on the table. The positional levels III, IV, and V, then, become multiples of 360.
| V | 144,000 ÷ 360 = 400 | 288,000 ÷ 360 = 800 | 432,000 ÷ 360 = 1,200 | etc. |
| IV | 7,200 ÷ 360 = 20 | 14,400 ÷ 360 = 40 | 21,600 ÷ 360 = 60 | etc. |
| III | 360 ÷ 360 = 1 | 720 ÷ 360 = 2 | 1,080 ÷ 360 = 3 | etc. |
Now, let us analyze the numbers appearing in the table. The numbers situated at positional level II may also be obtained by doubling the numbers corresponding to positional level I (1 - 20), and then simply adding a zero;
| 18 + 18 = 36 + 0 = 360 |
In other words, multiplying by the integer 20 can also be achieved by simply doubling the number and adding a zero to the product. Observe the positional values at levels I and II on the table of numbers:
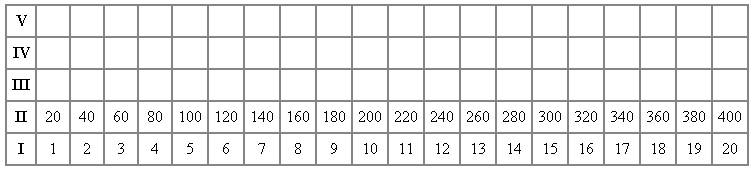
In each case, at each level and integer one can identify this possibility:
| 1 + 1 = 2 + 0 = 20 |
| 2 + 2 = 2 + 0 = 40 |
| 3 + 3 = 6 + 0 = 60 |
| etc. |
Now, observe that this same relationship does not exist between the values listed on positional levels II and III, since the difference between these two levels is 18; not 20. It would appear as though the calendar count has become interrupted, no longer following the integer 20 logic. It is not possible to simply double the number on level II and add a zero to it order to obtain the number on level III. By selecting the positional level to begin with 360, instead of the number 400 (20 x 20; the value on space 20), then the apparent logic has been broken.
However, as we examine levels III, IV and V, we now notice that the relationship of 20 does exist among these three levels. Again, instead of multiplying, one may revert to the procedure of doubling the corresponding number on the lower level to obtain the next higher level, and simply add a zero.

In order to make the translation from level II to level III, one would have to account for the two places (19 and 20) that were skipped, when the table was broken off at the value of 18 (360).
As a proposal for a method of calculation, let us run through a specific example.
For the sake of example, let us offer the case the number 15.
a) Take the number 15 and double it and add a zero to that sum:
| 15 + 15 = 30 + 0 = 300 | (= level II value) |
|
15 + 15 = 30 |
| 300 - 30 = 270 |
| 270 + 270 = 540 + 0 = 5400 | (= level III value) |
| 5400 + 5400 = 10800 + 0 = 108000 | (= level IV value) |
| 108000 + 108000 = 216000 + 0 = 2160000 | (= level V value) |
In this manner, one is able to obtain the corresponding numbers of each of the five positional levels on the Table of Numbers for the number 15:
| V | 2,160,000 |
| IV | 108,000 |
| III | 5,400 |
| II | 300 |
| I | 15 |
The method of calculation, without multiplication, for obtaining the corresponding numbers on the Table of Numbers for the 360-count, for each positional level can be summarized as follows:
Choose a number 1 to 20:
Example:
| 15 | double it and add a zero |
| 30 0 | subtract 10% from that |
| 27 0 | double it and add a zero |
| 540 0 | double it and add a zero |
| 1080 0 0 | double it and add a zero |
| 2160 0 0 0 | double it and add a zero |
| 4320 0 0 0 0 | double it and add a zero |
| 8640 0 0 0 0 0 | double it and add a zero |
| ad infinitum. | |
In this manner one can obtain any number series on the Table of Numbers, thereby reconstructing the entire table without actually having it written down, and without performing any long method of multiplication. Calculations into the millions or billions, and beyond, may be obtained with relative ease.
In the following part of this essay we shall now review the 360c reckoning with the old calendar 260, in order to perceive their possible relationship.
Part II
The 260 Day-Count
Over the millennia, much of ancient knowledge has been destroyed, both voluntarily and involuntarily through conquest. It is impossible to know exactly how much was destroyed. We may attempt, however, a recreation of the numerical tables that were understandably employed in calendar reckonings of ancient times. The Table of Numbers that we have discussed here might suggest the existence at one time of other tables of reckoning.
We have reviewed the counting system based on the integer twenty method, and the the multiplication of 18 x 20, which offers a pattern based on the cut-off point 360. The 360c has been related to the calendar round of 360 days, with the necessary remaining five days being added on (in maya the name for these five days is the uayeb; in nahuatl, it was nemonetemi).
But, there was an older calendar based on the 13 x 20 relation, producing the 260-day count (260c). This calendar of 13 months and twenty days existed within various cultures of Mexico. "We know that this 260-day cycle count of the days, called the tzolkin by the maya and tonalpohualli by the aztecs, lay at the core of all Mesoamerican calendars, at least since the sixth century B.C. This cycle rose to prominence, I think, because it approximated the length of several fundamental life-sustaining periods: It was a measure of the duration of the agricultural season, nine lunar months (266 days), as well as the Venus appearance interval ..., and it was equal to 13 x 20, both sacred numbers." (from Aveni, p.79).
We shall now consider what might have been the manner for reckoning the 260c in the light of the Table of Numbers (360c) presented in Part I.
We proceeded to follow the same logic of the integer 20 system as in the 18 x 20 (= 360c) calendar round, and devised the following 260c Table of Numbers:
| Mars | Mars | Mars | |||||||
| 104000 | 208000 | 312000 | 416000 | 520000 | 624000 | 728000 | 832000 | 936000 | 1040000 |
| 5200 | 10400 | 15600 | 20800 | 26000 | 31200 | 36400 | 41600 | 46800 | 52000 |
| 260 | 520 | 780 | 1040 | 1300 | 1560 | 1820 | 2080 | 2340 | 2600 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Mars | Mars | Mars | |||||||
| 1144000 | 1248000 | 1352000 | 1456000 | 1560000 | 1664000 | 1768000 | 1872000 | 1976000 | 2080000 |
| 57200 | 62400 | 67600 | 72800 | 78000 | 83200 | 88400 | 93600 | 98800 | 104000 |
| 2860 | 3120 | 3380 | 3640 | 3900 | 4160 | 4420 | 4680 | 4940 | 5200 |
| 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
In order to produce this table of number based on the 260c, there was
again no need to effect a single multiplication. The procedure that we
exemplified for calculating the numbers as shown earlier was employed.
Now, instead of using the number 360 as the cut-off point, the number 260 is used. It is significant to note that the numbers related to the 52 and 104 cycles, so important in ancient reckoning in Mexico, appear on the 260c Table of Numbers, although they do so in multiples. Remember that these numbers do not appear on the table of numbers of the 360c. The fact that the cycles of 52 (years) and 104 (years) may have come from the older calendar of the 260c reckoning would seem to be logical from an historical perspective. Nonetheless, those same cyclical periods remained relevant to the 360c.
Such a system of reckoning would then serve in making calculations of whole cycles between one calendar round and another. For, as some authors have pointed out, ancient cultures were very much concerned with identifying the relationships of the cosmos in terms of whole cycles: "The essence of this mathematically predictive astronomy consisted of the art of defining how many whole cycles of one set of phenomena accorded with how many of another set. Maya and late Babylonian astronomers alike were engaged in exploring and discovering commensurate numbers, embedded in nature, that described cycles of recurring phenomena: 99 moons and 5 Venus cycles, 151 Mars cycles and 284 years, the eclipse cycle of 223 moons and 19 seasonal years, and so on." (Aveni, p. 123).
A general belief existed that patterns existed in nature, and that these patterns could be and were expressed mathematically. In this sense, the Table of Numbers of the distinct calendar rounds (360c and 260c) reflect the systematic study of the solar system. The respective counting systems by their very logic of cut-off points are a product of that concern. Let us examine a specific relationship of equivalency between the 260c and 360c:
| 1872000 | ÷ | 260 | = | 7200 |
rounds | |
| 93600 | ÷ | 260 | = | 360 |
" | |
| 4680 | ÷ | 260 | = | 18 |
" | |
| 260 | ÷ | 260 | = | 1 |
" | |
| 13 | ÷ | 260 | = | .05 |
" | (= 1 day) |
| 1872000 | ÷ | 360 | = | 5200 |
rounds | |
| 93600 | ÷ | 360 | = | 260 |
" | |
| 4680 | ÷ | 360 | = | 13 |
" | |
| 260 | ÷ | 360 | = | .72222 |
" | |
| 13 | ÷ | 360 | = | .03611 |
" |
| Conversions: | 7200/260c = 5200/360c 18/260c = 13/360c |
Further considerations of an infinite number of time-cycle relationships could be as follows:
| 13 rounds of 360c | = | 18 rounds of 260c |
| = | 8 rounds of Venus (less 8 days) | |
| = | 6 rounds of Mars | |
| = | 158.5 lunar cycles (less .5 a day) | |
| etc. |
In other words, the relationships that exist in nature, as the planets revolve around the sun, in relation to one another, may be expressed numerically. This possibility seemed to convey a hidden meaning that could be revealed in the pattern of numbers themselves. Students of numerology might make it appear as though only the numbers are significant. But, let us remember that ultimately the relationships that are being measured and converted to numerical expression are what is important. But, the numbers, being the reflection of the relations, take on that same sacredness.
In order to better comprehend the numbers and the relations that they reflect, let us review the distinctions in the counting systems.
As was mentioned earlier, the cut-off point the Table of Numbers is the first place of the third positional level (III, 1). One might initially consider that the very distinction lies in the two system of multiplication; that of 13 x 20 and that of 18 x 20, which forms the distinguishing aspects of the two calendar counts. As we have explained, levels I and II are easily translated between themselves, and then, as a separate set, levels III, IV and V are translatable among themselves. And, note that this occurs equally on the 260c calendar, although the cut-off point is now distinct (260c; not 360c). Furthermore, now all of the levels III, IV and V are divisible by the number 260.
The Table of Numbers, then, as it must have been originally designed, can accommodate any number of an orbital cycle (or day-count), of any particular planet (or moon,s orbit), in order to create a set of numbers relevant to that astronomical body. In a very real sense, then, not just a numbering system or a counting system was created by the 13 x 20 or the 18 x 20 reckonings, but the basis for creating astronomical tables was developed through a method of procedure as we have attempted to show.
Hence, it is at the positional level of III, 1 that the time-cycle number of 360 or 260 may be substituted for that of the orbital time of any other planet. Now, since the Table of Numbers functions on the basis of the integer 20 (as one of its main multipliers), then it is necessary to maintain that the chosen orbital day-count number be an even number (divisible by 20), while the other main multiplier may be any even/odd integer.
Let us now substitute the 260c and the 360c numbers for those relating to other planets in the solar system that were considered to have been known then.
Part III
The Day-Counts of Venus, Mars, Jupiter, Saturn , and Mercury; the Earth's Moon
In this section we shall offer the different day counts that refer to the planets Venus, Mars, Jupiter, Saturn and Mercury, alongwith that of the Earth,s moon. After having produced the Table of Numbers for the 260c, a generic, non-orbital count, of astronomical significance, we consider that similar tables of numbers may be created for each of the planets' and the Moon. The day-counts of the different planets, orbits are in terms of the 365-day orbit of earth, expressed therefore in terms of their synodic revolutions; the time that it takes a planet to revolve around the sun on its orbit and return to its point of departure. (It is understood that the planet never returns to its exact position in space, but to the same orbital position relative to the sun/earth relationship).
In order to produce the Tables of Numbers of the different planets, we shall employ the following data and considerations:
| Planet/body | Multipliers | Calendar Reckoning | Actual Orbit Days/round |
| Earth Seasonal Year |
18 x 20 | 360c | 365.2421987 |
| Earth Astronomical Year |
13 x 20 | 260c | (365.2421987) |
| Venus | 29 x 20 | 580c | 584 (583.92) |
| Mars | 39 x 20 | 780c | 780 |
| Jupiter | 20 x 20 | 400c | 398.8846 |
| Saturn | 19 x 20 | 380c | 378.0919 |
| Mercury | (5.75 x 20) | 115c | 115.8774 |
| The Moon | 1.5 x 20 | 30c | 29.53058857 |
For the reckonings in the different tables, we have chosen the numbers
closest to the actual orbital day-counts. The fractional differences will
be treated in the tables of the additional day-count numbers (either through
addition or subtraction).
In the frist six cases listed above, the number 20 is employed as a principal multiplier alongwith an even/odd integer. While in the case of Mercury and the Moon, the integer 20 is accompanied by a fractional number (5.75 and 1.5 respectively), given the fact that we have chosen a day-count number as close as possible to their orbital numbers. However, these fractions pose no special problems in the calculations, because as we stated earlier, only addition is involved in the procedure.
| 260 | |||||||||||||||||||
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 360 | |||||||||||||||||||
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 580 | |||||||||||||||||||
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 30 | |||||||||||||||||||
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 115 | |||||||||||||||||||
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 780 | |||||||||||||||||||
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
The multipliers, although definitely determinant for the time-cycles expressed
in the values of the table, are implied aspects that remain somewhat outside
of the picture. To make them more visible, we shall offer a Table of Calendar
Rounds, which will offer the count for each specific positional level
and place (i.e., I - V, and 1 - 20). For each Table of Numbers is based
on the same number of calendar rounds (proportionately to each level/place),
as we shall observe later.
Now, let us examine each Table of Numbers for the particular planets that we have selected for the analysis.
| 232000 | 464000 | 696000 | 928000 | 1160000 | 1392000 | 1624000 | 1856000 | 2088000 | 2320000 |
| 11600 | 23200 | 34800 | 46400 | 58000 | 69600 | 81200 | 92800 | 104400 | 116000 |
| 580 | 1160 | 1740 | 2320 | 2900 | 3480 | 4060 | 4640 | 5220 | 5800 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2552000 | 2784000 | 3016000 | 3248000 | 3480000 | 3712000 | 3944000 | 4176000 | 4408000 | 4640000 |
| 127600 | 139200 | 150800 | 162400 | 174000 | 185600 | 197200 | 208800 | 220400 | 232000 |
| 6380 | 6960 | 7540 | 8120 | 8700 | 9280 | 9860 | 10440 | 11020 | 11600 |
| 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
For the planet Venus, we have chosen the 580c to produce the Table of Numbers, since its orbital rotation value is generally accepted as 584 days, although it is specifically 583.92 days. However, we shall attempt to work without the fractions, in order to be able to comprehend the whole cycle relationships better. Furthermore, this probably follows the general rule of thumb of ancient astronomy which conceived of the relationship between the orbits of Venus and Earth as constituting a 5:8 ratio.
| 312000 | 624000 | 936000 | 1248000 | 1560000 | 1872000 | 2184000 | 2496000 | 2808000 | 3120000 |
| 15600 | 31200 | 46800 | 62400 | 78000 | 93600 | 109200 | 124800 | 140400 | 156000 |
| 780 | 1560 | 2340 | 3120 | 3900 | 4680 | 5460 | 6240 | 7020 | 7800 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 342000 | 3744000 | 4056000 | 4368000 | 4680000 | 4992000 | 5304000 | 5616000 | 5928000 | 6240000 |
| 171600 | 187200 | 202800 | 218400 | 234000 | 249600 | 265200 | 280800 | 296400 | 312000 |
| 8580 | 93600 | 10140 | 10920 | 11700 | 12480 | 13260 | 14040 | 14820 | 15600 |
| 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 152000 | 304000 | 456000 | 608000 | 760000 | 912000 | 1064000 | 1216000 | 1368000 | 1520000 |
| 7600 | 15200 | 22800 | 30400 | 38000 | 45600 | 53200 | 60800 | 68400 | 76000 |
| 380 | 760 | 1140 | 1520 | 1900 | 2280 | 2660 | 3040 | 3420 | 3800 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1672000 | 1824000 | 1876000 | 2128000 | 2280000 | 2432000 | 2584000 | 2736000 | 2888000 | 3040000 |
| 83600 | 91200 | 98800 | 106400 | 114000 | 121600 | 129200 | 136800 | 144400 | 152000 |
| 4180 | 4560 | 4940 | 5320 | 5700 | 6080 | 6460 | 6840 | 7220 | 7600 |
| 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 46000 | 92000 | 138000 | 184000 | 230000 | 276000 | 322000 | 368000 | 414000 | 460000 |
| 2300 | 4600 | 6900 | 9200 | 11500 | 13800 | 16100 | 18400 | 20700 | 23000 |
| 115 | 230 | 345 | 460 | 575 | 690 | 805 | 920 | 1035 | 1150 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 506000 | 552000 | 598000 | 644000 | 690000 | 736000 | 782000 | 828000 | 874000 | 920000 |
| 25300 | 27600 | 29900 | 32200 | 34500 | 36800 | 39100 | 41400 | 43700 | 46000 |
| 1265 | 1380 | 1495 | 1610 | 1725 | 1840 | 1955 | 2070 | 2185 | 2300 |
| 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 12000 | 24000 | 36000 | 48000 | 60000 | 72000 | 84000 | 96000 | 108000 | 120000 |
| 600 | 1200 | 1800 | 2400 | 3000 | 3600 | 4200 | 4800 | 5400 | 6000 |
| 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 132000 | 144000 | 156000 | 168000 | 180000 | 192000 | 204000 | 216000 | 228000 | 240000 |
| 6600 | 7200 | 7800 | 8400 | 9000 | 9600 | 10200 | 10800 | 11400 | 12000 |
| 330 | 360 | 390 | 420 | 450 | 480 | 510 | 540 | 570 | 600 |
| 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
THE TABLE OF ADDITIONAL DAYS
We shall now offer a table of numbers regarding the additional days that are required for calculating some of the planets' time-cycles. Again the same logic of the Table of Numbers is followed. However, we have listed this table according to the calendar rounds in absolute numbers of whole cycles of 1 - 8000, with respect to the additional numbers of days of 1 - 6. For example, 6 additional days would be required to reach the 266c from the 260c; 5 additional days for the 365c from the 360c, as well as the 6 days for leap year; 4 additional days are required for the 584c coming from the Venus 580c; etc.
One would simply have to know the whole cycle numbers of the main count, and then consult the same number of cycles and the respective number of additional days required.
| Days | Rounds 4400 | 4800 | 5200 | 5600 | 6000 | 6400 | 6800 | 7200 | 7600 | 8000 |
| 6 | 26400 | 28800 | 31200 | 33600 | 36000 | 38400 | 40800 | 43200 | 45600 | 48000 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 22000 | 24000 | 26000 | 28000 | 30000 | 32000 | 34000 | 36000 | 38000 | 40000 |
| 4 | 17600 | 19200 | 20800 | 22400 | 24000 | 25600 | 27200 | 28800 | 30400 | 32000 |
| 3 | 13200 | 14400 | 15600 | 16800 | 18000 | 19200 | 20400 | 21600 | 22800 | 24010 |
| 2 | 8800 | 9600 | 10400 | 11200 | 12000 | 12800 | 17600 | 14400 | 15200 | 16000 |
| Days | Rounds 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 | 3600 | 4000 |
| 6 | 2400 | 4800 | 7200 | 9600 | 12000 | 14400 | 16800 | 19200 | 21600 | 24000 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 2000 | 4000 | 6000 | 8000 | 10000 | 12000 | 14000 | 16000 | 18000 | 20000 |
| 4 | 1600 | 3200 | 4800 | 6400 | 8000 | 9600 | 11200 | 12800 | 14400 | 16000 |
| 3 | 1200 | 2400 | 3600 | 4800 | 6000 | 7200 | 8400 | 9600 | 10800 | 21000 |
| 2 | 800 | 1600 | 2400 | 3200 | 4000 | 4800 | 5600 | 6400 | 7200 | 8000 |
| Days | Rounds 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 6 | 1320 | 1440 | 1560 | 1680 | 1800 | 1920 | 2040 | 2160 | 2280 | 2400 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1100 | 1200 | 1300 | 1400 | 1500 | 1600 | 1700 | 1800 | 1900 | 2000 |
| 4 | 880 | 960 | 1040 | 1120 | 1200 | 1280 | 1360 | 1440 | 1520 | 1600 |
| 3 | 640 | 700 | 740 | 780 | 840 | 900 | 960 | 1020 | 1080 | 1140 |
| 2 | 440 | 480 | 520 | 560 | 600 | 640 | 680 | 720 | 760 | 800 |
| Days | Rounds 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| 6 | 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | 1080 | 1200 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| 4 | 80 | 160 | 240 | 320 | 400 | 480 | 560 | 640 | 720 | 800 |
| 3 | 60 | 120 | 180 | 240 | 300 | 360 | 420 | 480 | 540 | 600 |
| 2 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| Days | Rounds 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 6 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 4 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 3 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 2 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| Days | Rounds 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
THE TABLE OF CALENDAR ROUNDS
This table of numbers offers the whole cycle numbers that are implied in each one of the Tables of Numbers for the specific day-count that we have offered in this study. In each Table of Numbers, the corresponding cut-off day-count (30c, 115c, 260c, 360c, 584c, etc.) becomes a constant for that table's calculation, inasmuch as the positional levels of III, IV and V are divisible by that respective day-count number. Each specific level and place represent an absolute number of calendar rounds (or orbital rotations of a particular astronomical body, except the non-orbital amount of 260c). The number of days in the count may change, but the number of calendar rounds, then, remains constant for the table of numbers.
| Rounds: | 4400 | 4800 | 5200 | 5600 | 6000 | 6400 | 6800 | 7200 | 7600 | 8000 |
| 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 | 3600 | 4000 | |
| 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 | |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Days: | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
From the previous chart, it is evident that the set of constant numbers
of rounds (or whole cycles) may reflect all numerical possibilities to
infinity. For within the addition of the numbers listed from 1 to 8,000
calendar rounds, one could feasibly extend the table of numbers to any
level beyond V. Furthermore, although the number 500 calendar rounds is
not listed on the table of numbers and calendar rounds, one may simply
add the value of 400 rounds to that of 100, and with that one would obtain
the corresponding 500-rounds value. The possibilities are limitless.
It should now be obvious, that with the astronomical Tables of Numbers as presented, one coulds ompare almost any possible set of time-cycles and calendar reckonings with respect to the astronomical bodies treated herein. The whole-cycle patterns are readily visible through simple addition and subtraction.
Observations
Tables of numbers do exist within the maya culture in ancient Mexico. One has only to examine the Dresden Codex which has been interpreted as a registration of the movement of Venus and corresponding eclipses. Although we may never find exact example of the Tables of Numbers cited herein, the tables reflect the procedure implied in the 18 x 20 and 13 x 20 calendar reckonings. In fact, the 260c and the 360c calendar reckonings are themselves already the product of related calculations.
Multiplication is ultimately a form of addition. The Tables of Numbers, as illustrated in this essay, through their method of calculation, do not require a multiplication procedure; simple addition is sufficient to effect the calculations. The counting of time-cycles seems to take for granted a system of counting; something that is often overlooked. Furthermore, the ancient concept of time-cycles and the comparison of whole cycles, becomes more profound as we contemplate the relationship of one year to that of millions of days. Such a comparison, in itself, reflects a profound degree of human consciousness, that we still have difficulty in comprehending ourselves. In other words, if the ancient peoples represented numerically millions of days, then they consciously thought in terms of thousands of years.
The significant aspect, then, might not be that they abstracted time-cycles into seven or eight-digit numbers, but rather that they abstracted the progression of time through mathematics. The simplicity in calculation reflects a complexity of mental conceptualization that in turn implies a need for such extensive calculations. Such calculations were probably not only necessary for the sowing and harvesting of crops, but possibly dealt with a greater knowledge of the Cosmos; a knowledge that we have yet to discover completely.
Reproduction prohibited without written consent of the author.
Your comments and suggestions are greatly appreciated:
e-mail: johnson@earthmatrix.com
Science in Ancient Artwork Number One
The Integer (20) Calendar Reckoning and Astronomical Tables: Ancient Mexico
January 1995
1995-2014 Copyrighted by Charles W. Johnson. All Rights Reserved
Earth/matriX,
| Home | Books | Forum | Reviews | All Essays | Author |