

The Pythagorean Theorem:
|
| 32 | + | 42 | = | 52 |
| 9 | + | 16 | = | 25 |
| 25 | = | 25 |
In this manner, one obtains an equivalency that allows knowing the relationship between the two legs of the right triangle and the hypotenuse. In the case of perfect right triangles, the resulting numbers are whole numbers (no fractional expressions). Other perfect right triangles concern the series, 5•12•13, whose numbers are as follows:
| 52 | + | 122 | = | 132 |
| 25 | + | 144 | = | 169 |
| 169 | = | 169 |
The numbers that exist are those of the side measurements of the (perfect) right triangles. The interesting point of the previous examples is to recognize that the 144c and the 169c are ancient reckoning counts (for example, 144, 288, 576…; and, 169, 338, 676…). The 25 is a constant number series (25, 50, 100, 200, 400, 800…) also employed in the ancient reckoning system. And, one must also recognize the fact that the 3 • 4 • 5 counts reflect ancient reckoning counts.
The Pythagorean Theorem, based upon the squaring of the side measurements of the right triangle, serves as a method for obtaining one of the unknown sides thereof. In the case of a right triangle (not a perfect one), fractional expressions would obtain, as in the following example.
| 5 | + | 13 | = | ? |
| 52 | + | 132 | = | ? |
| 25 | + | 169 | = | ? |
| 194 | = | ? | ||
| |
= | 13.92838828 |
13.92838828 being the side measurement of the hypotenuse a the
5 • 13 • 13.92838828 right triangle
The only numbers, in the above procedure, that actually reflect spacetime/motion events are those that relate to the side measurements of the right triangle:
5, 13, and 13.92838828
Whereas, the other numbers, 25, 169 and 194 are procedural numbers in the computation and do not reflect or represent any spacetime/motion event (other than that relating to the Pythagorean procedure in computational mathematics).
Problems arise when the procedural numbers are given life, or thought to be representative of something that actually exists in reality. The relationship that is then ignored or misapprehended is the essential one relating to the hypotenuse to the leg measurements of the right triangle. For example, let us see what is happening in relation to the 3 • 4 • 5 perfect right triangle in these terms.
The essential relationship within the 3 • 4 • 5 perfect right triangle may be better visualized as of the diagonal line within a rectangle.

If we add up the values relating to the perimeter of the rectangle (3 + 4 + 3 + 4), we obtain the value of 14.
| 14 | / | 5 | = | 2.8 |
| 5 | / | 14 | = | .357142857 |
In other words, the perimeter is 2.8 times greater than its diagonal line, or the diagonal line is only .357142857th of the perimeter, as shown.
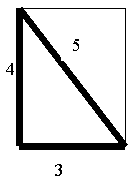
The previous observation also applies to the perfect right triangle itself.
The sums of the two legs of the perfect right triangle shown are 1.4 times greater than the hypotenuse; and, the hypotenuse is now .714285714th of the sum of the two legs of that same perfect right triangle.
We cannot find an unknown value within the right triangle by simply finding the simple sum of the values of the side measurements:
3 + 4 = 7 (not 5, which is the value of the hypotenuse)
So, the squares of the numbers provide a translation of the sum figure of seven into the next level of poetic values of equivalency.
3 + 4 = 7 ( not 5)
hence,
| 32 | + | 42 | = | 52 |
| 9 | + | 16 | = | 25 |
| 25 | = | 25 |
The squares of the numbers are elevating the terms to an equivalency based upon the relationship between the values of 25 and 7.
25 / 7 = 3.571428571
The actual relationship that exists pertains to the 5 : 7 ratio of the diagonal (hypotenuse) to the sides of the rectangle (triangle).
| 5 | / | 7 |
=
|
.714285714 |
| 3 | + | 4 |
|
5 |
| 3 | + | 4 |
=
|
7 |
| 9 | + | 16 |
=
|
25 |
| 7 |
|
25 | ||
| 25 | / | 7 |
=
|
3.571428571 |
The sum of the two legs of the perfect right triangle, in this case, is 3.57142857ths of the poetic number 25 relating to the squares of the values of the two legs (or to the square of the value of the hypotenuse). The poetic value of 3.571428571 is five times the actual value of the relationship between the hypotenuse (5) and the sum of the two legs (7) of the perfect right triangle under consideration.
3.571428571 / .71428571 = 5.000000002
The procedural squaring of the values of the (perfect) right triangle has simply created an adjustment of values of equivalency. The recognition of the distinct nature of the values within the Pythagorean Theorem shall become significant in our comprehension of the ancient reckoning systems.
In the case illustrated above, two aspects become relevant for the ancient reckoning system. First, the 28c represents and ancient reckoning count, and, secondly, the relationships of equivalency for the side measurements and the diagonal line of the rectangle shown are significant for computations based on the reciprocal of the number seven (.142857).
Jefferson, Louisiana
Revised February, 2002
e-mail: johnson@earthmatrix.com
More links
©2002-2013 Copyrighted by Charles William Johnson.
All rights reserved. Reproduction Prohibited.
Earth/matriX.
SCIENCE IN ANCIENT ARTWORK
SCIENCE TODAY SERIES.
| Home | Books | Forum | Links | Author | All Essays |