The Reckoning Systems of Ancient Mesoamerica
day-count and constant numbers

Introduction

The significant numbers of the reckoning systems of ancient Mesoamerica consist of day/year count numbers, cycle numbers, and constants. These numbers appear to form a logically structured system, which serve as the basis for the different reckoning systems of ancient Mesoamerica. The day/year counts that reflect the orbital times of the planetary bodies are accompanied by cycle counts, which may also represent day/year counts. For example, the 365 day-count (365c) and the 584 day-count (584c) of Earth and Venus respectively, are accompanied by the cycle counts of 52 and 65, or 104 and 65, again respectively. These cycle-count numbers may also represent days or years themselves in the method of calculation devised by the ancient astronomers.

Furthermore, the system consists of constant numbers, such as multiples of 8 and 5, derived from the relation of Earth's eight orbits to Venus' 5 synodic orbits; and, inversely, from the relation of Venus' 8 sidereal orbits to Earth's five orbits.

In this case, the cycle numbers represent constant numbers, which may be employed to obtain equivalencies in the day-counts.

In this manner, one may understand the reason for the 360c within the maya long count system may be due, then, to its relationship to the 225c sidereal count of Venus' orbit, whereby the relation 225/360 enjoys the same relation as 365/584, which is .625.

In earlier essays (Earth/matriX Nos. 8 & 12), we have attempted to show how the relationship between the 365c and the 584c may have established the origin of the 260c calendar of ancient Mesoamerica. For the comparison of these two day-count systems (365 & 584c) produce a year-cycle relation, whereby day equivalencies between the two occur on a scale of 260 years and 416 years. In other words, every 260 years of the 584c correspond to day-count equivalencies every 416 years on the 365c system.

In this essay, we shall attempt to establish the relationship that exists, then, regarding the 260c calendar in terms of the synodic and sidereal orbital, times of Venus (respectively, 584c and 225c), with respect to Earth's solar year (365c). In order to do this, we must identify the cycle numbers that correspond to the 260c system. In a previous essay (Earth/matriX No. 8), we attempted to distinguish the 260c with a 73-year cycle.

In this sense, the 146/260c system corresponds to the 65/584c system and to the 104/365c system:

This relationship reveals, then, the correspondence among these systems, whereby calculations based on the 146/260c system would refer to the synodic orbital time of Venus (584c).

We must now understand what might be the corresponding cycle number to the 260c system when it refers to the sidereal orbital time of Venus (225c). In order to do so, we shall have to consider the 260c system in terms of the 65/360c and 104/225c systems cited above.

It would appear, then, that the maya long count number (360c) was designed in order to achieve calculations regarding an approximation between Earth's solar year and Venus' sidereal orbital time, in relation to the reckoning system of 52/365:65/584:73/260; as well as, in relation to calculations of Venus' orbital time of its synodic year based on a 585c. By the use of these day-count numbers, cycle-numbers, and constants, general (and even precise) calculations could be made regarding whole cycles of the planetary bodies involved. In further essays, we shall see how these reckoning systems, in fact, accounted for calculations regarding the orbital time of the Moon (lunations; full lunar cycles; etc.).

The 90/260c System

As we have mentioned earlier, with regard to the 584c system, the 260c system appears to have been based on a cycle number of 73, since that number offers calculations of equivalencies of day-counts with regard to the 365c system of Earth. The 73-cycle number refers to calculations in reference to the synodic orbital time of Venus (584c). With regard to the sidereal orbital time of Venus, the cycle number for the 260c appears to have been 90:

For the 90 cycles of the 260c are equal to 104 cycles of the 225c; both equaling 23400 days. In other words, for calculations concerning the synodic 584 day-count of Venus, one would employ a cycle number of 73; and for the sidereal 225 day-count of Venus, one would use a cycle number of 90.

The two distinct reckoning systems, at the level of their method of calculation, would consist of the following day-counts, and cycle numbers (or year-cycles):

Now, within the 90/260c reckoning system, which corresponds to calculations regarding the maya long count system of 65/360c, the valence for Venus' synodic orbital time would be calculated on the basis of the 585c.

In other words, in order to make a translation from the maya long count, based on the 65/360c and the 104/225c (Venus' sidereal orbital time), one would simply employ a 585c for Venus' synodic orbital time. Then, whole cycles among the different systems could be easily attained. Given that the cycle of orbital time of Venus varies by a couple of days, it is understandable that one could work with distinct valences, making the necessary adjustments from the 585c to the average 584c.

From these numbers one may observe the logic of design in having selected the 225:360c relation, in relation to the 585c of Venus' synodic orbital time as a possible method of calculation for obtaining whole cycles among Venus' synodic and sidereal years as a function of Earth's solar year (360 maya long count). Furthermore, this allows for a translation with the 260c calendar as well.

The tzolkin of the 260 day-count functions evenly with the numbers of days listed above:

As we have already shown partially, the tun of the 360c relates equally well to these numbers:

From the above, one may observe that on the 260c whole cycle numbers would be obtained every 23400 days; while on the 360c, whole cycle numbers would appear every 46800 days (46800 divided by 360 = 130c).

In this manner, one may have calculated rapidly that:

Such an obvious equivalency of cycle numbers in relation to the maya long count, may well represent the method of calculation behind the perceived logic of numbers. While it remains obvious that the 365c number against these numbers does not allow for obtaining whole cycles:

The 365c is a function of the reckoning system identified earlier, regarding the 65/584c of Venus and the 104/365c of Earth's solar year, in relation to the 146/260c system.

With such and obvious logic of numbers regarding the 360c and its relationship to the 225c of Venus, one might conclude that the 360c was not in fact an error of measurement, but quite the opposite: the result of an exact astronomical understanding of the orbital times of the Earth and Venus, as well as of the Moon.

The 2704 cycle count

Let us take the previously cited numbers derived from the 23400 number of days. This number reflects 104 sideral orbits of Venus (225c), and 40 synodic orbits of Venus. Let us invert this, whereby there are 104 synodic orbits of Venus:

Now, let us divide this number of days by the other counts:

The 270.4 number appears to be significant, and relevant to other calculations that may be implied in some of the ancient artwork of Mesoamerica, sucha as the Aztec Calendar. As we have seen the day-counts and the cycle numbers, alongwith the constant numbers, may be interchanged, with their corresponding valences changing as well. Hence, we have emphasized how a particular number (i.e., 65, 104, etc.) does not represent an absolute value, but is relational to the events and the reckoning system under consideration.

In our previous analysis of the elements of the Aztec Calendar (Earth/matriX Nos. 2, 4, 5, etc.), we have emphasized the point that the elements of the Aztec Calendar may have distinct valences, relational to the reckoning system being considered. However, aside from this relational aspect of assigning values to the calendar's elements, we also drew attention to the fact as to how, many scholars have suggested the existence of certain elements which are not actually sculped on the image of the Aztec Calendar, but implied by its design. Such was the case of the Ring of Quincunxes.

The number of elements of the quincunx figure is apprently forty (40) in number. From our study of the design of the quincunx figure, we suggested that possibly one could allow the quincunx to represent the binding of the years, the 52-year cycle. Obviously, it could also represent the 65-year cycle of Venus, given that the quincunx figure among the maya people represented the planet Venus. However, as we have seen, the cycle numbers (52, 65, 104, etc.) are interchangeable, depending upon whether one is measuring cycles of the synodic orbit of Venus or of its sidereal orbit.

In a previous essay (Earth/matriX No. 10), it was pointed out that possibly the Ring of Quincunxes could represent the value of 2080 years (40 x 52 = 2080). Other scholars have suggested that possibly the Ring of Quincunxes consists of 52 quincunx elements, given the possibility that the design suggests there to be 3 quincunx elements beneath each of the four solar rays on that ring. In this case, there would be 52 quincunx elements on the Aztec Calendar's Ring of Quincunxes. A most significant calculation obtain then, if that were the case, or if that constituted a theoretically abstracted alternative for making calculations. For, at the assigned value of 52-years/quincunx, the ring would enjoy a valence of 2704 total years.

Now, let us take a day-count from the 365c and the 584c, which is cited in the Dresden Codex, a count of 37960 days. With this example, and the previous one, it is rather obvious that the interrelatedness of the different systems follows a stric logic in agreement with the day-count numbers, the cycle numbers, and the constant numbers, as we have been attempting to illustrate. Such would appear to be the basis for achieving calculations of whole cycles among the different planetary bodies. Consider a few examples in relation to the 37960 day-count number:

The number of relations that one might explore appear to be infinite in nature, whereby one may obtain equivalencies of day-counts, cycles and constants, then the differences between these numbers, etc. The numbers that represent the day-counts, the cycles, and the constants may themselves be assigned distinct valences in the translation from one system to another. In the face of such a designed system of numbers, it should become clear that the interpretation of the different reckoning systems' numbers can only be relational. There would appear to exist no absolute, exclusive interpretation of a particular number. The context within which the particular number is then situated would appear to become all determinant for its comprehension to be exact.

The Constant Numbers

The manner in which the reckoning systems flow from one into the other may be better observed from the Table of Constant Numbers that we presented in an earlier essay (Earth/matriX No. 17). In this table, it may observed how the maya long count numbers appear on the table alongwith the day-count numbers, the tzolkin number, the tun, the lunar cycle numbers, the constant numbers in distinct manners of presentation, among others. Therefore, the reckoning systems would appear to consist of the day/year-count numbers, the cycle numbers, and the constant numbers, all of which often repeat themselves within one another.

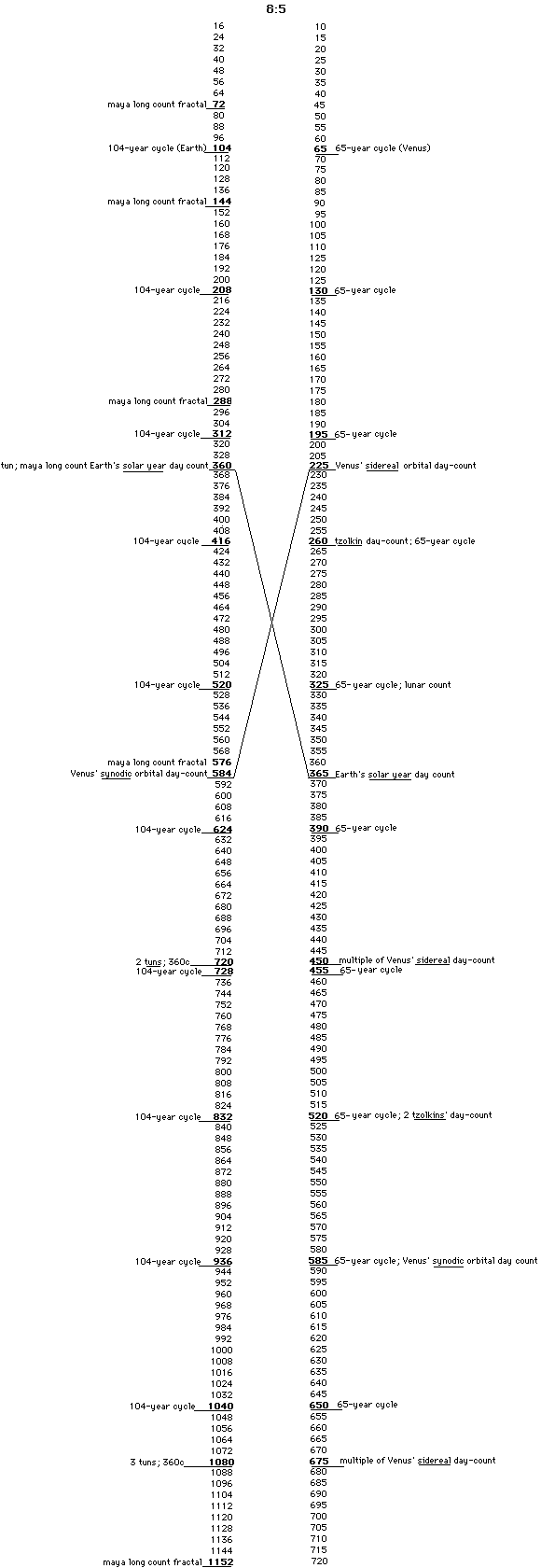From this table, one may observe that the same number appears at times on either side of the scale. For example, this occurs with the numbers 360 and 520. However, from the logic of the table, one might realize that the 360c of the tun would appear logically on the side of the maya long count fractals, with regard to the doubling of the constant number 8. Such would be the case with the 520 number that occurs on the side that refers to the doubling of 8, whereby it follows the sequence of the 52-cycle count. Although, 520 on the right side of the doubling of the number 5 would refer to 2 tzolkins (2 x 260).

One must then take care in understanding the possible meaning of each number in relation to the numbers with which it forms a sequential ppatern, and not extract it from its context. In other words, the Table of Constants has a logic of its own, which would appear to be reflected in the calculations that are possible in the different reckoning systems. Therefore, for example, the number 520 is relational to the number 832 or the number 325, which are immediately across from it on either scale. In order to comprehend the meaning then of the 520 number, one would have to consider the sequential pattern represented by the 832 number (104-year cycle pattern), and the 325 number (65-year cycle pattern).

Other patterns become available, and calculations become difficult to discern. For example, the number 9344 appears in the Dresden Codex table of numbers referring to the different phases of Venus (236, 90, 250, 8). The number 9344 represents 16 orbits of Venus' synodic count (584 c). However, consider the following fractal that may be developed as of the Table of Constants by relating the different day-counts:

Hence, 584 years of the 584c equals 934.4 years of the 365c. By knowing such relationships, one could read the Dresden Codex numbers on the Venus table of phases in a very distinct manner; knowing that 9344 years of the 365 equal 5840 years of the 584c.

Innumerable examples are readily available. Consider for example the following. In the Dresden Codex the example of 65 orbits of 584c of Venus is given as 37960 days:

The above could be read as:

The readings and calculations, as we have mentioned, are infinite given the design of the ancient reckoning systems of Mesoamerica.

Observations

The reckoning systems of ancient Mesoamerica appear to be based on day/year count numbers, cycle numbers, and constants, as perceived by many different scholars. However, the design of the distinct reckoning systems, based on these different kinds of numbers reveal the possibiblity of making calculations of whole cycles in time, regarding the distinct orbital times of the planetary bodies according to the design of the reckoning systems themselves.

In other words, the specific day-counts of 260c and 360c, respectively the tzolkin and the tun, are numbers chosen by design, based on the relations perceived by the ancient astronomers of the planetary bodies. The numbers 260c and 360c do not represent errors in calculation, but relational, mathematical constants themselves, which may be employed for making the translation from the sidereal and synodic orbits of Venus to the solar year of Earth's orbit (365c). Also, the specific reckoning systems allow for calculations of other bodies, such as the Moon, and we shall be dealing with these calculations in later essays.

In our research, we have attempted to illustrate how the 260c system is related to, and derived from, the 365c and the 584c in their combined relationship to one another. The 360c, it should be clear, is related to and derived from, the 225c and the 585c of Venus, in relation to the 365c as well through specific methods of calculation.

The Table of Constant Numbers that we have shown regarding the duplatio method of the relation 8:5 (and also that of 16:10 implied therein), reflects the possibility to achieve all of the relevant numbers of the ancient reckoning systems as developed in Mesoamerica. From this one chart, by doubling the retio 8:5, one may observe all of the day/year counts, the cycle numbers, and the constants themselves. It would appear to be almost incredible that such a relationship between abstracted numerical constants and numbers that reflect actual events in the solar system would have such a strict relationship.

From the Table of Constant Numbers, it would be possible to teach younger scholars how to retain and know all of these numbers simply from the duplatio method being applied to the relation 8:5 of the orbits of Earth and Venus. In fact, as we have seen, from that one would know the synodic and the sidereal orbits of Venus. The Table of Constant Numbers, in this light, represents an entire textbook of astronomy.