Earth/matriX
Science in Ancient Artwork
and
Science Today
Serie No 101
Trigono/metriX:
The Trigonometric Table
and Ancient Reckoning
By
Charles William Johnson
|
Trigono/metriX: The Trigonometric Table
and Ancient Reckoning
Introduction
One of the most difficult aspects of high-school education deals with teaching the trigonometric table of ratios for triangles, their relations of degrees and side measurements. However, with contemporary electronic calculators, the simple push of a sin, cos,or tan button now eliminates a lot of headaches. Nonetheless, students must still attempt to deal with this particular table, whose complete comprehension is not always fully achieved.
Today, many scholars have a difficult time considering the possibility that the ancient cultures knew anything regarding mathematics over and above simple addition and subtraction. Hardly any scholar accepts their having considered something like trigonometry. Yet, as we review the logic of the historically significant numbers, time and again, we observe how those numbers reflect different aspects of what we today refer to as higher mathematics. With regard to the trigonometric table of ratios, the findings are no different; it would appear as though the ancient cultures may have even chosen some of those historically significant numbers (eg., 189, 288, 1872, 2268, etc.), as of that very table of ratios.
In this essay, we shall offer a more complete look at the trigonometric table of ratios, by filling in all of the possible ratios for relationships of the sides of triangles. It appears that the commonly found table at the back of most textbooks on trigonometry does not offer the complete set of possibilities for those enunciated ratios. And, we shall examine how the numbers of the ratios relate and suggest different aspects of the historically significant numbers of the ancient reckoning system.
The Trigonometric Ratios
The trigonometric ratios of a triangle generally are presented as of the sine, cosine, and tangent of a particular angle thereof. These concepts deal with the relationship between two sides of a triangle.
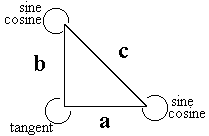
The sine and cosine relations reflect those of the two acute angles of a triangle, while the tangent reflects the relations of the right angle. The ratios regarding these particular relations are then generally listed on a "Table of Trigonometric Ratios"at the end of most textbooks on the subject. The ratios are usually presented in the form of decimal place numbers, generally to the fourth decimal place.
In order to use such a table, one may employ these decimal numbers for computing the side measurements and number of degrees within a particular angle of a right triangle. As one may observe from the following table, the degrees are offered usually in whole numbers, whereby one must compute precisely the degrees/minutes/seconds in a particular angle. With contemporary electronic calculators, one must simply press a button in order to obtain such results. However, the reader should note that only six columns of numbers are generally offered, which reflect, in fact, only four distinct relationships of the sides of triangles and their angles.
| Rad | Deg | Sin | Cos | Tan | Csc | Sec | Cot | ||
|---|---|---|---|---|---|---|---|---|---|
| .0000 | 00 | .0000 | 1.0000 | .0000 | ----- | 1.0000 | ----- | 90 | 1.5707 |
| .0175 | 01 | .0175 | .9998 | .0175 | 57.2987 | 1.0002 | 57.2900 | 89 | 1.5533 |
| .0349 | 02 | .0349 | .9994 | .0349 | 28.6537 | 1.0006 | 28.6363 | 88 | 1.5359 |
| .0524 | 03 | .0523 | .9986 | .0524 | 19.1073 | 1.0014 | 19.0811 | 87 | 1.5184 |
| .0698 | 04 | .0698 | .9976 | .0699 | 14.3356 | 1.0024 | 14.3007 | 86 | 1.5010 |
| .0873 | 05 | .0872 | .9962 | .0875 | 11.4737 | 1.0038 | 11.4301 | 85 | 1.4835 |
| .1047 | 06 | .1045 | .9945 | .1051 | 9.5668 | 1.0055 | 9.5144 | 84 | 1.4661 |
| .1222 | 07 | .1219 | .9925 | .1228 | 8.2055 | 1.0075 | 8.1443 | 83 | 1.4486 |
| .1396 | 08 | .1392 | .9903 | .1405 | 7.1853 | 1.0098 | 7.1154 | 82 | 1.4312 |
| .1571 | 09 | .1564 | .9877 | .1584 | 6.3925 | 1.0125 | 6.3138 | 81 | 1.4137 |
| .1745 | 10 | .1736 | .9848 | .1763 | 5.7588 | 1.0154 | 5.6713 | 80 | 1.3953 |
| .1920 | 11 | .1908 | .9816 | .1944 | 5.2408 | 1.0187 | 5.1446 | 79 | 1.3788 |
| .2094 | 12 | .2079 | .9781 | .2126 | 4.8097 | 1.0223 | 4.7046 | 78 | 1.3614 |
| .2269 | 13 | .2250 | .9744 | .2309 | 4.4454 | 1.0263 | 4.3315 | 77 | 1.3439 |
| .2443 | 14 | .2419 | .9703 | .2493 | 4.1336 | 1.0306 | 4.0108 | 76 | 1.3265 |
| .2618 | 15 | .2588 | .9659 | .2679 | 3.8637 | 1.0353 | 3.7321 | 75 | 1.3090 |
| .2793 | 16 | .2756 | .9613 | .2867 | 3.6280 | 1.0403 | 3.4874 | 74 | 1.2915 |
| .2967 | 17 | .2924 | .9563 | .3057 | 3.4203 | 1.0457 | 3.2709 | 73 | 1.2741 |
| .3142 | 18 | .3090 | .9511 | .3249 | 3.2361 | 1.0515 | 3.0777 | 72 | 1.2566 |
| .3316 | 19 | .3256 | .9455 | .3443 | 3.0716 | 1.0576 | 2.9042 | 71 | 1.2392 |
| .3491 | 20 | .3420 | .9397 | .3640 | 2.9238 | 1.0642 | 2.7475 | 70 | 1.2217 |
| .3665 | 21 | .3584 | .9336 | .3839 | 2.7904 | 1.0711 | 2.6051 | 69 | 1.2043 |
| .3840 | 22 | .3746 | .9272 | .4040 | 2.6695 | 1.0785 | 2.4751 | 68 | 1.1868 |
| .4014 | 23 | .3907 | .9205 | .4245 | 2.5593 | 1.0864 | 2.3559 | 67 | 1.1694 |
| .4189 | 24 | .4067 | .9135 | .4452 | 2.4586 |
1.0946 | 2.2460 | 66 | 1.1519 |
| .4363 | 25 | .4226 | .9063 | .4663 | 2.3662 | 1.1034 | 2.1445 | 65 | 1.1345 |
| .4538 | 26 | .4384 | .8988 | .4877 | 2.2812 | 1.1126 | 2.0503 | 64 | 1.1170 |
| .4712 | 27 | .4540 | .8910 | .5095 | 2.2027 | 1.1223 | 1.9626 | 63 | 1.0996 |
| .4887 | 28 | .4695 | .8829 | .5317 | 2.1301 | 1.1326 | 1.8807 | 62 | 1.0821 |
Depending upon the angle being computed, the different concepts reflect distinct relationships of the sides of a triangle. For example, in a triangle of 30:60:90-degrees, the following is understood:
| sine 30° | involves the relation | a/c |
| cosine 30° | b/c | |
| sine 60° | b/c | |
| cosine 60° | a/c | |
| tangent 30° | a/b | |
| tangent 60° | b/a |
Immediately, one realizes that the previous relations do not represent all possible
ratios for the sides of a triangle. The missing relations are: c/a
and c/b.
The generally cited table of trigonometric ratios offers the following data for the 30:60:90-degree relationships:
| a/c | b/c | a/b | b/c | a/c | b/a | ||
| Angle | sine | cosine | tangent | Angle | sine | cosine | tangent |
| 30° | .5000 | .8660 | .5774 | 60° | .8660 | .5000 | 1.7321 |
One possible reason for so much confusion may be attributed to the fact that
in these concepts a single term represents different relations. In other words,
the sine of 30° is the cosine of 60°;
and, the sine of 60° is the cosine of 30°.No
wonder confusion characterizes this particular aspect of trigonometry.
Given this particular fact, one could simply reduce the expression of the table of trigonometric ratios by offering only that data which is useful in the computations and which is not repeated. In this manner one could devise a table that would consist of the four main relations for computing the relationships among the sides of a triangle and its angles; knowing that sine and cosine interchange in a specific way. Such a summary view of the table of trigonometric ratios may be presented in the following manner.
(Summary view)
|
The complete table would be as follows:
Table of Trigono/metriX Ratios
Ratios
| Degrees/Ratios: | ||||||
|---|---|---|---|---|---|---|
| (a/c) | (b/c) | a/b) | c/b | (b/a) | c/a | |
| 0:90:90° | ||||||
| 1:89:90 | 017452406 | 999847695 | 017455065 | 1.000152357 | 57.28996163 | 57.29868993 |
| 2 : 88 | 034899497 | 999390827 | 034920769 | 1.000609536 | 28.63625328 | 28.6537081 |
| 3 : 87 | 052335956 | 998629535 | 052407779 | 1.001372351 | 19.08113669 | 19.1073227 |
| 4 : 86 | 069756474 | 99756405 | 069926812 | 1.002441894 | 14.30066626 | 14.33558697 |
| 5 : 85 | 087155743 | 996194698 | 087488664 | 1.003819835 | 11.4300523 | 11.47371321 |
| 6 : 84 | 104528463 | 994521895 | 105104235 | 1.005508282 | 9.514364454 | 9.566772258 |
| 7 : 83 | 121869343 | 992546152 | 122784561 | 1.007509829 | 8.144346428 | 8.205509075 |
| 8 : 82 | 139173101 | 990268069 | 140540835 | 1.009827572 | 7.115369722 | 7.185296532 |
| 9 : 81 | 156434465 | 987688341 | 15838444 | 1.012465126 | 6.313751515 | 6.392453223 |
| 10 : 80 | 173648178 | 984807753 | 176326981 | 1.01542661 | 5.67128182 | 5.758770472 |
| 11 : 79 | 190808995 | 981627183 | 194380309 | 1.018716697 | 5.144554016 | 5.240843075 |
| 12 : 78 | 207911691 | 978147601 | 212556562 | 1.022340594 | 4.70463011 | 4.809734341 |
| 13 : 77 | 224951054 | 974370065 | 230868191 | 1.026304109 | 4.331475874 | 4.445411489 |
| 14 : 76 | 241921896 | 970295726 | 249328003 | 1.030613628 | 4.010780934 | 4.133565488 |
| 15 : 75 | 258819045 | 965925826 | 267949192 | 1.035276181 | 3.732050808 | 3.863703307 |
| 16 : 74 | 275637356 | 961261696 | 286745386 | 1.040299435 | 3.487414444 | 3.627955276 |
| 17 : 73 | 292371705 | 956304756 | 305730681 | 1.045691756 | 3.270852618 | 3.420303617 |
| 18 : 72 | 309016994 | 951056516 | 324919696 | 1.051462225 | 3.077683539 | 3.236067981 |
| 19 : 71 | 325568154 | 945518576 | 344327613 | 1.057620683 | 2.904210878 | 3.071553491 |
| 20 : 70 | 342020143 | 939692621 | 363970234 | 1.064177774 | 2.747477419 | 2.923804403 |
| 21 : 69 | 35836795 | 933580426 | 383864035 | 1.071144992 | 2.605089065 | 2.790428106 |
| 22 : 68 | 374606593 | 927183855 | 404026226 | 1.078534744 | 2.475086853 | 2.669467166 |
| 23 : 67 | 390731128 | 920504853 | 424474816 | 1.086360379 | 2.355852366 | 2.559304668 |
| 24 : 66 | 406736643 | 913545458 | 445228685 | 1.094636279 | 2.246036774 | 2.458593336 |
| 25 :65 | 422618262 | 906307787 | 466307658 | 1.103377918 | 2.144506921 | 2.366201582 |
| 26 : 64 | 438371147 | 898794046 | 487732589 | 1.11260194 | 2.050303842 | 2.281172032 |
| 27 : 63 | 4539905 | 891006524 | 509525449 | 1.122326237 | 1.962610506 | 2.202689263 |
| 28 : 62 | 469471563 | 882947593 | 531709432 | 1.13257005 | 1.880726465 | 2.130054467 |
| 29 : 61 | 48480962 | 874619707 | 554309051 | 1.143354069 | 1.804047755 | 2.062665341 |
| 30 : 60 | 5.0 | 866025404 | 577350269 | 1.154700538 | 1.732050808 | 2.0 |
| 31 : 59 | 515038075 | 857167301 | 600860619 | 1.166633397 | 1.664279482 | 1.941604026 |
| 32 : 58 | 529919264 | 848048096 | 624869352 | 1.179178404 | 1.600334529 | 1.887079916 |
| 33 : 57 | 544639035 | 838760568 | 649407593 | 1.192363293 | 1.539864964 | 1.836078459 |
| 34 : 56 | 559192903 | 829037573 | 674508517 | 1.206217949 | 1.482560969 | 1.788291651 |
| 35 : 55 | 573576436 | 819152044 | 700207538 | 1.220774589 | 1.428148007 | 1.743446797 |
| 36 : 54 | 587785252 | 809016994 | 726542528 | 1.191264217 | 1.428148007 | 1.701301618 |
| 37 : 53 | 601815023 | 79863551 | 75355405 | 1.207252229 | 1.37638192 | 1.661640142 |
| 38 : 52 | 615661475 | 788010754 | 781285627 | 1.223974669 | 1.327044822 | 1.624269246 |
| 39 : 51 | 629320391 | 777145961 | 809784033 | 1.24147515 | 1.279941632 | 1.589015729 |
| 40 : 50 | 64278761 | 766044443 | 839099631 | 1.259800314 | 1.234897157 | 1.555723826 |
| 41 : 49 | 656059029 | 75470958 | 869286738 | 1.279000202 | 1.191753593 | 1.524253087 |
| 42 : 48 | 669130506 | 743144825 | 900404044 | 1.29912884 | 1.150368407 | 1.494476774 |
| 43 : 47 | 68199836 | 731353702 | 932515086 | 1.320243709 | 1.110612515 | 1.466279186 |
| 44 : 46 | 69465837 | 7193398 | 965688775 | 1.342408191 | 1.07236871 | 1.439556541 |
| 45 : 45 | 707106781 | 707106781 | 1.0000000 | 1.414213563 | 1.0000000 | 1.414213563 |
The same scope of computations may be obtained by employing either of the two previously shown tables of trigonometric ratios. The "summary view" may be even further reduced as occurs on a contemporary electronic calculator, which employs only three buttons to be pressed: sin, cos, tan. But, the full-blown version offers the student a complete idea of all of the possible relationships among the different sides of a triangle and the ratios produced thereof in relation to the angles in whole numbers.
By listing the relation of angles for each ratio, instead of simply placing only one particular angle, one may better comprehend the very relationships of the angles within the right triangle. When we speak about a 30-degree angle within a right triangle, we are evidently implying a 30:60:90-degree relationship. Therefore, the table should always suggest that particular aspect. The complete "Table of Trigono/metriX Ratios" thereby conveys more precisely what is occurring within these relationships. And, in order to obtain precise results, one must necessarily compute with a greater number of decimal places than four (as found on most tables of trigonometric ratios). Exact computations cannot be achieved with only four decimal places.
For example, on a 5:12:13 perfect right triangle consider these computations on an electronic calculator, where the corresponding side measurements are:
| 1800 : 4320 : 4680 | ||
| 4320/4680 = .92307692307 | ||
| 4680 x .9230 = 4319.64 | 4680 x .92307692 = 4319.9999856 | |
| but, | 4680 x .92307692307 = 4319.99999996 |
The four decimal computation falls far short of an approximation to the computations
involved in this case. The limitations of a conventional "table of trigonometric
ratios" become obvious with these computations.
Now, let us observe how the Table of Trigono/metriX Ratios relates to the historically significant numbers of the ancient reckoning systems.
The Ancient Reckoning Systems and
the Table of Trigono/metriX Ratios
Of the numerous aspects that appear between the ancient reckoning systems and the Table of Trigono/metriX Ratios, we shall limit our analysis to only a few main ones. Other aspects shall be dealt with in later essays, but for now we shall concentrate on those aspects which may suggest the possibility that the historically significant numbers of the ancient reckoning systems may have been chosen as of a knowledge of trigonometry.
The ancients are said to have avoided fractions, yet their computations seem to suggest that they knew the fractions in a precise manner; hence, the seeking of whole numbers. One cannot seek whole numbers without knowing the fractions/decimals. Aside from this aspect of the ancient reckoning procedures, the numbers themselves are suggestive of those associated with the table of trigonometric ratios.
Some historically significant numbers of the relations of degrees that become immediately outstanding on the Table of Trigono/metriX Ratios are the following:
| 1 : 89 | (kemi number series: 189, 378, 756) | |
| 2 : 88 | (maya long count series: 144, 288, 576, 1152, 2304) | |
| ... | ||
| 5 : 85 | (Venus synodic fractal: 585) | |
| ... | ||
| 10 : 80 | (kemi count: 27, 54, 108, 216, 432) | |
| ... | ||
| 18 : 72 | (maya long count fractal: 1872000) | |
| ... | ||
| 22: 68 | (Nineveh number: 2268) | |
| ... |
From the very start, by listing the relationships of degrees of triangles on this particular table, one is able to observe relationships of degrees that produce numbers which resemble some historically significant numbers. These numbers/fractals coming out of the relationships of degrees in right triangles are based upon a 90-based system (0 : 90 : 90; or, a total of 180 degrees in a triangle).
Many different aspects become available. Consider the sum of the first few numbers on the list:
| 189 + 288 + 387 = 864 | and | 864 / 2 = 432 (the Consecration) |
| 189 + 288 + 387 + 486 + | 585 + | 684 + 783 =3402 (...108864 series) |
Or, consider how if one adds all of the numbers from 189 until and including
the 2268 number, the total is 27027; the mirrored kemi count (27c).
By choosing the 2268 number, one could understand how the 27c could have been
encoded into the ancient reckoning system. Therefore, by drawing attention to
the 22:68 relation, the significance of the 27c is established.
From the above, one may observe how the naturally occurring numbers serve as the basis for some of the historically significant numbers.
Obviously, one might constantly attribute such relationships to mere coincidence. But, the coincidences continue to increase. Consider the fact that a 3 : 4 : 5 right triangle, which has been cited as having been employed in the design of ancient artwork involves angles which reflect the maya long count numbers/fractals.

As we apply the mediatio/duplatio procedure to the 36.8699-degree angle, the following reveals itself:
| 36.8699 | |
| 18.43495 | |
| 9.217475 | |
| 4.6087375 | |
| 2.30436875 | |
| 1.152184375 | |
| .576092188 | |
| .288046094 | |
| .144023047 | (here, the maya fractals appear double with the sacred 9) |
| .072011523 | |
| .036005763 | |
| .018002881 | |
| .00900144 |
The previous series of numbers is characteristic of naturally occurring numbers
regarding a 3 : 4 : 5 right triangle. The fact that the ancient maya
chose a number system based on the series 36, 72, 144, 288, 576, 1152, 2304,
and, the fact that these numbers appear within the angle of a 3:4:5 right triangle,
plus the fact that the maya appear to have employed just such
a triangle in the design of some of their ancient artwork, together would seem
to be a product of a conscious design.
Further consider the fact that when one divides the angle 36.8699° by the number three, instead of two, one may observe an apparent relationship with the maya companion number, 1366560.
| 36.8699 / 3 | = | 12.28996667 |
| 4.096655556 | ||
| 1.365551852 (now, take whole number/fractal) | ||
| 1365550 - | 1365560 | = 1010 |
Just how significant may the 3:4:5 right triangle be for the ancient reckoning system may be understood when we assign the number 13c to its sides measurements:
| 3 x 13 = 39 | 4 x 13 = 52 | 5 x 13 = 65 |
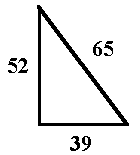 |
Consider, then, 39 x 52 = 2028; whereby 2028 is a chosen number
found in the total number of years for the Legend of Four Suns of ancient Mesoamerican
cultures. But, not only that, in the 3:4:5 relation, one may symbolically and
computationally comprehend the 39c constant number count of the ancient reckoning
system, along with the 52c year cycle, and, the 65c year-cycle for Venus of
ancient Mesoamerican systems. These three significant counts are then found
together in the numbers of the 3:4:5 right triangle.
One can imagine the ancients being concerned with right triangles that reflect whole numbers in their angles (eg., the 30:60:90-degree right triangle); or, whole numbers in their side measurements (eg., the 3:4:5 right triangle). As of this particular knowledge, they most undoubtedly understood that no apparent triangle existed which could enjoy whole numbers in both aspects, in its angles and side measurements combined. They may have achieved this, however, through symbolic representation; hence, the significance of number series in the ancient reckoning systems of the world.
This could have been achieved through the remainder mathematics that seems to have characterized some of the ancient systems of reckoning. For example, instead of employing the .1732 decimal number for the 30:60:90 right triangle, they could have used the 1728 constant-number series, and added/subtracted corresponding sums as they moved up and down the series. The 30:60:90 right triangle is essentially a 1 : 2 : 3 side measurements triangle. In order to visualize this triangle symbolically as a 1:2:3 triangle, one could simply employ the 1728 constant-number series for the side that measures the number/fractal three, compensating with the corresponding addition and/or subtraction amount to reach 1732 (1732 - 1728 = 4).
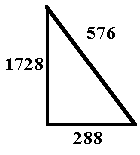
Let us illustrate this point with a 288c base number:
| 1 x 288 = 288 | 2 x 288 = 576 | 3 x 288 = 1728 | |
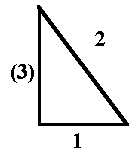 |
 |
||
In this manner, the 30:60:90 right triangle may visually represent a triangle with 1:2:3 side measurements, although, we know that this is not so in reality. One could then convert later to the exact corresponding measurement:
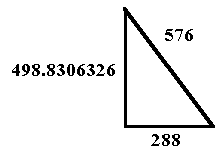
This triangle could thus serve as a teaching/learning tool for the numbers of the ancient reckoning system.
The numbers become evidently significant when employed in the Pythagorean Theorem formula:
| 2882 + 17282 = | 3068928 | ||||
| 3068928 | - | 5762 | = | 2737152 | |
| 2737152 / 2 = | 1368576 | ||||
| - 1366560 | |||||
| 216 | |||||
| 4032 | |||||
| 1008c |
The 1728c number becomes all important in some computations. Further consider the numbers/fractals cited here as of multiplication, and in relation to the ancient reckoning system number of Nineveh, (1959552c).
|
Then, other relations appear:
| 1728 | x | 567 | = | 979776 | (kemi; 567) |
| 1959552 | (Nineveh) | ||||
| 1732 | x | 576 | = | 997632 | (maya; 576) |
| - 995328 | |||||
| 2304 | (maya alautun) | ||||
| 1732 | x | 567 | = | 982044 | (kemi; 567) |
| - 979776 | |||||
| 2268 | (Nineveh) |
The 3:4:5 right triangle reveals further significance for the maya
long count system in that its numbers are more obvious:
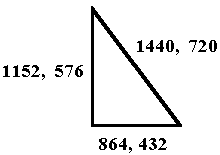
The side measurements of the 3:4:5 right triangle immediately reflect the number series of the maya long count on two sides, while reflecting the number series of the sacred 432 consecration number.
Observations
In this essay, we have illustrated two aspects of the measurement of right triangles. Firstly, we have shown how the table of trigonometric ratios for the sides and angles of right triangles, which is commonly cited in the literature, may be viewed as of the possible relationships involved in such computations.
Secondly, we have shown how some of the numbers/fractals associated with the table of trigonometric ratios reflect some of the historically significant numbers within the ancient reckoning systems. Time and again, we find that the historically significant numbers/fractals of the ancient reckoning systems share such common elements with the general traits of mathematics and geometry, that one can only conclude that much of ancient artwork may have been based on such knowledge.
The designs of ancient artwork appear to have a common cognitive base, founded upon the characteristics of geometry and mathematics, and in this case in particular, even within the field of trigonometry. The general table of trigonometric ratios has been expanded here to include all of the possible relations of right triangles in the measurement of their angles and sides. We have called this the Table of Trigono/metriX Ratios in order to distinguish this added knowledge from that generally presented on such tables.
Once again, as we observe ancient historically significant numbers, such as 1872 or 2268, we come to realize that possibly such numbers were read and treated in a manner distinct from which we have learned throughout the ages. The number 1872 and 2268 may not only represent day/year counts, but just possibly may reflect a reading that would suggest their representing the relations of degrees in a specific right triangle: 18:72:90, and, then, 22:68:90 degrees. When the ancients observed the number 2268, they may have also been viewing that number not only as 2268, but as 22 in relation to 68 [2268] (and, further in relation to 90 [226890]). Such a dynamic way of viewing and communicating numbers/fractals reaches beyond the more limited reading that we exercise today within mathematics and geometry.
©1998-2012 Copyrighted by Charles William Johnson. All rights reserved.
email: johnson@earthmatrix.com
Science in Ancient Artwork
Trigono/metriX: the Trigonometric Table and Ancient Reckoning
Nº.101
4 January 1998
© 1998-2012 Copyrighted by Charles William Johnson. All Rights Reserved
| Home | Forum | Author |
|
|