 |
E
a r t h / m a t r i X
|
|||||
The
Reciprocal of Seven and Pi( )
)
in the Ancient Reckoning System
| Introduction
The Relationship of Pi to the Different Day-Counts The Aztec Calendar: An Illustration of the Reciprocal of Seven Relationship in Design The Kemi/Sothic Cycle and the K'awil of the maya The Concept of Pi on the Aztec Calendar Observations |
The Reciprocal of Seven and Pi ( )
)
in the Ancient Reckoning System
Introduction
From our previous analyses of the ancient reckoning systems from around the world, it would appear as though they may have been a single system or, at least, relational to one another. In other words, the distinct systems may not have been developed in isolation from one another, but rather in strict relationship to one another. The different day-counts and the historically significant numbers appear to be easily relational to one another, as we have been illustrating throughout the Earth/matriX essays and extracts.
Two especially intriguing concepts within mathematics
and geometry concern the reciprocal of seven
(1 / 7 = .142857142857142857...), and, the relation of pi (![]() ), i.e.,
the diameter of a circle to its circumference. Today, on most electronic
calculators, pi is given as : 3.141592654; the number of times the diameter
of a circle may be divided into the circumference of a circle. Both of
these numbers represent unending decimal places. To date, mathematicians
attempt to carry the concept of pi to hundreds of thousands of decimal
places. For purposes of computation and all practicality, four decimal
places are more than sufficient (thousands of decimal places being simply
incommensurable).
), i.e.,
the diameter of a circle to its circumference. Today, on most electronic
calculators, pi is given as : 3.141592654; the number of times the diameter
of a circle may be divided into the circumference of a circle. Both of
these numbers represent unending decimal places. To date, mathematicians
attempt to carry the concept of pi to hundreds of thousands of decimal
places. For purposes of computation and all practicality, four decimal
places are more than sufficient (thousands of decimal places being simply
incommensurable).
Given the fact that these two numbers represent fractions with a decimal place, then one might conclude that the ancients avoided such numbers, given the fact that they appear to have worked only with whole numbers. From our analysis of the historically significant numbers and how these numbers relate within the different reckoning systems of the past, it may just be the case that these two numbers served as essential tools within the computational methods of those ancient systems. In other words, not only did the ancients not avoid these two numbers, but they may have employed them as the fundamental analytical instruments of their computational systems.
One of the initial problems to comprehending the ancient reckoning systems is to get past our own conceptual shortcomings. Our mathematical posits of today hinder our viewing the ancient systems as of their own terms. When we search for a particular concept or relation in numbers in the ancient systems, we do so as of our fixed concept of what pi may represent. As in all relationships, one may generally conceive of the elements of a circle from different viewpoints. For example, instead of fixing our sights on the relationship of pi as being a number as of the ratio diameter:circumference, we could simply employ the relational number of the diameter as a fixed amount, a constant. Once we do this, it then becomes obvious that the historically significant numbers take on their possible original meanings.
By assuming this perspective, we shall observe how the reciprocal of seven becomes directly relational to the concept of pi. Furthermore, we shall observe how the units of a circle may be contemplated as representing any chosen number. Today, when we think of a circle, we immediately consider the number 360 degrees. Yet, in previous essays (Cfr., Earth/matriX Nos. 87 & 89) we have analyzed the possibility of assigning a circle any number of degrees/units/segments (v.gr., 260c, 315c, 360c, 3744c, 378c, etc.). Once we come to realize that the number of segments/degrees making up a circle may vary, then it becomes obvious that the number assigned to pi shall also vary. Undoubtedly, the physical relationship of the diameter to the circumference of a circle does not vary (the diameter may only be divided into the circumference so many times and a fraction thereof); but, the numerical representation may vary as the numbers assigned to the degrees in a circle vary.
The different ancient reckoning systems (which may have represented a single system with distinct parts) appear to accomodate this particular idea. The historically significant numbers reflect just such a functioning in the computations. It is in such a manner that we shall speak about the possibility of the Nineveh number 2268 may represent the concept of pi (2.268) for a 260c circle.
The Relationship of Pi (![]() ) to the Different Day-Counts
) to the Different Day-Counts
Two historically significant day-counts concern the 360c day-count and the 260c day-count. Now, the 360c becomes immediately relevant to a circle as we know it, because we have historically assigned 360 degrees (units/segments) to a circle. We are not familiar with dealing with a circle that would consist of 260 degrees. We should have to rework and rethink our entire concept of mathematics and geometry.
Therefore, for a 360-degree circle, as we know it,
with any circle, any diameter and any corresponding circumference, the
concept of pi (![]() ) holds true for our computations. In other words, if the
diameter is taken to be one, then the circumference would be a measurable
3.141592654 (give or take a few thousand decimal places, depending on the
reader's concept of exactness in numbers). This may be represented as so
because, we have concluded today, that any diameter of a circle may be
divided 3.141592654 times into its circumference.
) holds true for our computations. In other words, if the
diameter is taken to be one, then the circumference would be a measurable
3.141592654 (give or take a few thousand decimal places, depending on the
reader's concept of exactness in numbers). This may be represented as so
because, we have concluded today, that any diameter of a circle may be
divided 3.141592654 times into its circumference.
The above numbers relate to any diameter and any
circle, with no specification of the number of degrees assigned to the
circle as such. Now, let us assign the circle 360 segments (or degrees).
In this case, the circumference of the circle consists of a measured 3.60
distance. Therefore, we may now divide the number corresponding to pi (![]() )
into the 360c number:
)
into the 360c number:
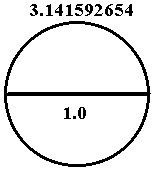
In such case, then, the diameter of a 360c circumference would be that of 1.14591559.
To summarize: a circumference of 3.141592654 would have a diameter of 1.0, whereby, a circumference of 3.60 would have have a diameter of 1.14591559.
Now, if we were to employ the 1.14591559 number (diameter) for a 260c circle, the following would obtain:
We may then observe how the Nineveh number (2268) makes it appearance in a fractional manner. Now, had the ancients actually employed the 2.268 number as pi for the 260c circle, the exact length of the diameter would be:
Note, that we are employing the numbers as fractals, and shall be doing so once again throughout this essay. We have already reached the conclusion that the historically significant numbers may have been employed to reflect day-counts, year-counts, cycle-counts, etc., and therefore the use of the decimal place was undoubtedly known in ancient times. Therefore, the diameter:circumference ratio may be conceptualized as either 114.638448:260.0 or, 1.14638448:2.60; etc.
 |
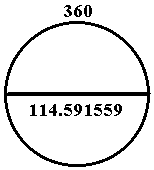 |
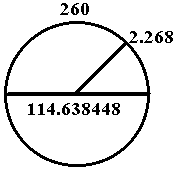 |
As we shall observe throughout this analysis, the different numerical relationships may simply reflect adjustments in the computations. Therefore, we may easily conceive of employing the 1.14638448 diameter for the 360c, whereby,
360 / 114.638448 = 3.14030769153 which would then represent a much lower number for the pi relationship as we have come to discern today.
Upon observing the modification of the number corresponding to the diameter, the reciprocal of seven immediately comes to mind in relation to the number eight:
Therefore, when we employ the reciprocal of seven (as an expression of 8/7) for the diameter of a circle, the following obtains for the 260c and the 360c numbers:
These numbers are relevant for the historically significant counts:
315, 630, 1260, 2520, 5040, 1008 and,
227.5, 455, 910, 1820, 3640 (the computational 364c day-count).
Further, consider: 315 x 360 = 1134, 2268
Now, given that 567, 1134, 2268, when doubled, we see that:
| 56.7 x 260 | = | 147242 | |||
If we employ the 114.638448 diameter for the 819c k'awil count, the following obtains:
but, if we employ the reciprocal of seven number which appears similar, then, the following obtains:
Given that: 936 / 819 = 1.142857143; we should also remember that: 260c x 360c = 93600, 187200.
Further considerations could involve: 3.15 / 2.268 = 1.388888889, which reminds us of the maya companion number 1385540. Therefore,
2.268 x 1.385540 = 3.14240472, which could have been an adjustment for the relationship of pi within the system.
If the number 3.15 were employed for pi, the its relationship to other historically significant numbers becomes evident as well. Consider another historically significant number from Nineveh: 19595520 fractal.
Now, take the Nineveh number and divide it by the maya companion number:
Another aspect to note is that the 360:2268 relation yields a mirrored number:
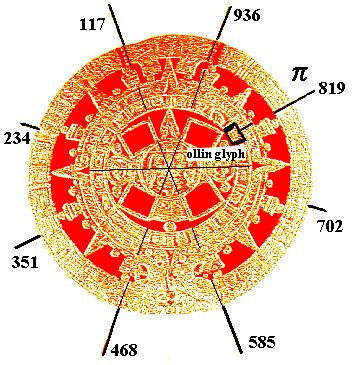
An infinite number of computations become available. A significant aspect for relating the mathematics to the geometry comes from observing the fact that the Aztec calendar (La piedra del sol), may have been based on a 7:8 ratio of segments, as we have analyzed in previous essays (Cfr., Earth/matriX, No.88). The ratio 8:7, as we have seen may have been representational of the concept of pi as of the fixed measurement (constant) of the diameter for a 260c and a 360c circle, by employing the reciprocal of seven numbers (1.142857). The reciprocal of seven would allow for computations of the 260c and the 360c, with the corresponding numbers for pi being 2.275 and 3.15. In this manner, it becomes clear that the 364c would have been the computational system of choice for the relationship of these two systems (the 364c being derived from the 2.275 number).
From this set of postulates, it then becomes relatively easy to understand that the ancient 364c and the 378c of ancient kemi could have been related to the 260c and the 360c by way of the reciprocal of seven as well. We have noted in previous analyses how the 52c year-cycle of ancient Mesoamerica and the 54c year-count of the kemi appear to be related. the reciprocal of seven helps us view this relationship better.
Furthermore, consider how the 416c cycle, well-known in ancient Mesoamerica appears as of the 364c and the reciprocal of seven, as well as the Consecration number as of the 378c and the reciprocal of seven:
This would also reveal the 693c relationship encoded into the Sothic cycle calendar which we have discussed previously (Cfr., Earth/matriX No 73)
| x | ||||||
| x | ||||||
Again, the computations become infinite, whereby all of the historically significant numbers may be accomodated within the system related to the reciprocal of seven and the different values for pi, depending upon the different number of segments/degrees that a circle may be assigned.
In summary, if a circle's diameter were assigned the number/unit one (1.0), then the circumference may be approximately 3.141592654.
If a circle's circumference is assigned the number 360c measurement, then its diameter would be 114.591559 (employing the base circle's measurement as pi, 3.141592654).
If a circle's circumference is assigned the number 260c measurement, then its diameter would be 114.638448 (employing the base circle's measurement as pi, 2.268).
From that any number of adjustments may be considered. Whereby, if we employ the diameter measurement to be a reciprocal of seven number (for example, 1.142857), on those particular circumference measurements, then the results would change as well.
If a circle's circumference is assigned the number 360c measurement, and its diameter measurement is taken to be theoretically 114.2857 , then the corresponding pi measurement would be 3.15.
If a circle's circumference is assigned the number 260c measurement, and its diameter measurement is taken to be theoretically 114.2857, then the corresponding pi measurement would be 2.275000284.
In this manner, the reciprocal-seven-like number, 1.142857 may be employed as the equivalent to the unit (diameter) one (1.0), for any circle's circumference (260c, 360c, etc.).
The Aztec Calendar: An Illustration of the Reciprocal of Seven Relationship in Design
One could imagine the number 3.15 being employed
as an approximation for pi (![]() ) in relation to a 360c circumference of a
circle. The 8:7 ratio would also become significant in this manner for
illustrating the geometry, and this may explain the reason why the Aztec
Calendar appears to present a spatial division based on the 7:8 or 8:7
ratios, as we have explained previously (Cfr., Earth/matriX No.88)
) in relation to a 360c circumference of a
circle. The 8:7 ratio would also become significant in this manner for
illustrating the geometry, and this may explain the reason why the Aztec
Calendar appears to present a spatial division based on the 7:8 or 8:7
ratios, as we have explained previously (Cfr., Earth/matriX No.88)
Furthermore, consider:
| = | |||
Therefore, if we view the Aztec Calendar as portraying the 315c and the 360c, then we are also viewing the 2268c Nineveh count (given that, 315 x 360 = 113400, 226800). And, as we have seen, when we view the 2268c, we are in relation to the ancient 260c as well. And, we already know that all of these counts, through the historically significant numbers, also reflect the computational 364c of the ancient reckoning system.
In the contemporary view of the concept of pi (![]() ),
we would conceive of the circle as a fixed set of relationship of numbers,
as of the diameter to the circumference of the circle:
),
we would conceive of the circle as a fixed set of relationship of numbers,
as of the diameter to the circumference of the circle:
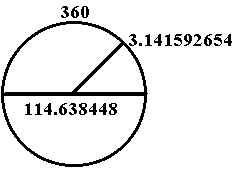
However, if we wish to change the numbers of the length of the diameter and the distance of the circumference, then the use of the reciprocal of seven becomes significant.
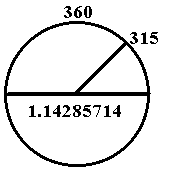 |
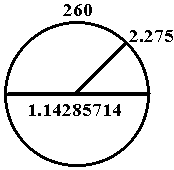 |
In this manner, the reciprocal of seven becomes relational to many other historically significant numbers. Consider,
One cannot help but notice that the 3168 number has been assigned to Jesus Christ throughout history.
It would appear as though the ancients were using the proportions of
pi (![]() ) in a modified manner, as of the approximations afforded by the reciprocal
of seven. Consider the following computation just for the sake of example
and the ease with which computations becomes available:
) in a modified manner, as of the approximations afforded by the reciprocal
of seven. Consider the following computation just for the sake of example
and the ease with which computations becomes available:
Or, consider the Venus counts:
Or, consider the Platonic Cycle:
Possibly, the computations for the Platonic Cycle, then, may have been based upon a conceptualization of the Earth's Great Cycle as of the reciprocal of seven and the Nineveh pi figure for a conceptual circle of 260 degrees/units (remembering that the Earth's Precession has been theoretically clocked at 26000 years).
In this sense, 22,680 years would be to 26,000 years, what pi (![]() ) is
approximately to a 360c circle. Furthermore, consider the Platonic cycle
number 25920 - 22680 = 3240, 6480, 12960 (kemi series).
) is
approximately to a 360c circle. Furthermore, consider the Platonic cycle
number 25920 - 22680 = 3240, 6480, 12960 (kemi series).
A similar result could be obtained going the other way, then, as of the 315:360 relationship.
The Kemi/Sothic Cycle and the K'awil of the maya
Consider one more possible reciprocal-seven computation that deals with different historically significant numbers coming from two different systems, that of the ancient kemi and the ancient maya.
The final number on this series reminds us of the number encoded in the Sothic cycle calendar: 164.9457812, which we have analyzed previously (Cfr., Earth/matriX No. 73). Now, consider the difference between these two apparently unrelated numbers:
The difference between the two apparently unrelated numbers ressembles the maya period of 151840 days, found in the maya companion number:
Once again, different historically significant numbers, from diverse ancient reckoning systems, neatly fit into place among themselves as of the reciprocal of seven.
The Concept of Pi on the Aztec Calendar
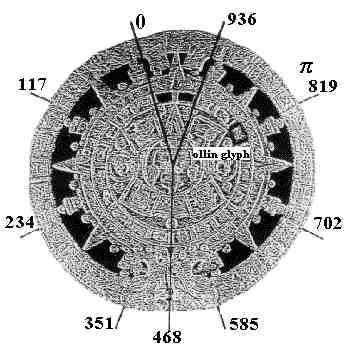
The Aztec Calendar may be conceptualized and visualized simultaneously as an eight-segment circle, as well as a seven-segment circle. It wre as though the very 8:7 design were communicating the concept of pi. This becomes further apparent when we consider that the ollin day-glyph, representing movement, falls exactly upon the 7:8 relationship. It were as though the very concept of the pi of pi were being communicated.
In this manner, there are distinct ways in which the historically significant numbers may correspondend to the elements of the design. If we distribute the numbers in the following manner, then, the glyph for the ollin becomes relevant, corresponding thus to the 819c k'awil count on a 936c circumference.
The 936c Circumference of the Aztec Calendar,
the Ollin and Pi

This same relationship may be visualized in another manner, as of the 117c of Venus.
The variations are infinite in scope. Let us employ the .864 percentage (2 x 432), instead of the .875 percentage (7/8), for the concept of pi
Again, the 311040 number has been identified in the ancient systems of China and Mesoamerica. One could imagine an adjustment pertaining, then, to the use of a symbolic pi of 3.1140, fo rexample, in order to obtain computations relevant to specific day-counts. This would be further significant, because the use of the .864 ratio regarding the 260c day-count also becomes relevant.
And, also relevant would be using a circle based on
Both the 2268 and the 1959552 fractal numbers have been cited as being historically significant Nineveh numbers. According to the relationaships of pi to the circle, 195.9552 would represent the pi-relation for a 226.8c circle/circumference, whereby the diameter measurement would be 115.7407407.
The concept of pi as a relational constant of fractions, could be any number of adjustments:
Observations
The number of times that the length of the diameter of a circle may divide into the distance of the circumference of the circle has been shown to be 3.141592654 times in current studies. However, if we consider the length of the diameter to represent the unit one (1.0), it becomes almost impossible to manage the number of segments within a circle.
Therefore, if we divide a circle into 260 or 360
segments (or degrees), as we imagine the ancients to have done, then the
number corresponding to the proportion of pi (![]() ) shall also vary; depending
precisely upon the number of degrees or segments into which the circle
has been divided.
) shall also vary; depending
precisely upon the number of degrees or segments into which the circle
has been divided.
The number 3.1416 was employed for many years, until greater precision has been achieved as of electronic computations. The relation 360 / 5.15 = 114.28571428 reveals a close approximation; and, further, 22 / 7 = 3.142857 is another historically significant example. These last two involve the reciprocal of seven. If we exchange the unit one (1.0) measurement for the diameter of any circle for that of 1.142857 (a reciprocal-seven number), then many of the historically significant numbers become extremely relevant and computationally relational among themselves.
We should note that the actual measurement of a straight
line (the diameter) and a curved line (the circumference) is unachievable.
The minute bending, no matter how minute, one way or the other, from a
straight line to a curved line, or from a curved line to a straight line,
shall always make an exact measurement an impossibility. Only an approximation
is possible. Therefore, the practical use of thousands of decimal places
is in fact impractical. In fact, regarding the very postulates concerning
pi (![]() ) we are always speaking about theoretical postulates. Only in theory
can the diameter of a circle be divided into the circumference of a circle;
not in reality. This point becomes significant since such a theoretical
comprehension would be necessary to comprehend the theoretical postulates
behind the exchange of numbers as suggested in the computations for the
ancient reckoning systems.
) we are always speaking about theoretical postulates. Only in theory
can the diameter of a circle be divided into the circumference of a circle;
not in reality. This point becomes significant since such a theoretical
comprehension would be necessary to comprehend the theoretical postulates
behind the exchange of numbers as suggested in the computations for the
ancient reckoning systems.
Ultimately, the ancient could employ any number they chose, that is assign any number to any particular geometrical figure, and still translate back and forth from one system to another. In other words, even though one might employ the 1.0 unit, or the 1.14638448 number, or the 1.142857 number or, even the 1.14591559 figure of contemporary mathematics, the reckoner would still know how to translate back and forth between systems with relative ease. For that concept of remainder math and the method of doubling/halving the numbers are extremely suited.
Just as one may employ the concept of pi (![]() ) as of
the constant ratio of the diameter:circumference for computations; one
could also have employed as an equally relevant constant as of the length
of the diameter; or, as of the length/distance of the circumference. All
three numbers represent, in fact, mathematical constants as of that particular
geometrical relationship.
) as of
the constant ratio of the diameter:circumference for computations; one
could also have employed as an equally relevant constant as of the length
of the diameter; or, as of the length/distance of the circumference. All
three numbers represent, in fact, mathematical constants as of that particular
geometrical relationship.
As of the circumference (ca., 260c, 360c, 378c, etc.), the length of the diameter (ca., 1.0, 1.142857, 1.14638448, etc.) will always yield a particular constant ratio (ca., 3.1416, 3.141592654, 3.15, etc.). The numbers may be interchanged; the relations remain the same. The ancients appear to have managed the concept of pi from its distinct variables (the length of the diameter, the distance of the circumference, and the relationship between these two); and, not just from the perspective of the relationship of the diameter:circumference as we do today.
Therefore, if the ancients employed an historically significant number for the ratio between the diameter and the circumference (pi), such as 3.15 or 2.268 (Nineveh), then the other variables (diameter and circumference measurements) would change accordingly. If they employed the reciprocal of seven (1.142857) for the length of the diameter, then the other variables (circumference and, diameter:circumference measurements) would change. If they assigned a specific number to the circumference (a day-count of 260, 360, 378, etc.), then the other two variables (diameter and, diameter:circumference) would change accordingly.
Depending upon which particular aspect of the circle the ancients may have been dealing with at the time, the numbers that became significant would be singled out accordingly. In this manner, instead of employing the diameter of a circle as unit one (1.0), in fact, the unit one would become the reciprocal of seven number 1.142857 (or, 8/7; eight sevenths). It is in this understanding that the Aztec calendar, for example, reveals a spatial division based upon the ratio 7:8 or 8:7; which, in fact, is a reflection of the concept of pi in many more diverse aspects than we generally conceive today. By employing the reciprocal of seven number (1.142857) for the diameter's length, the circle could then be divided into any number of segments (degrees) that one might wish. And, the incredible point would be that one would be essentially dealing with whole numbers in the computations through the reciprocal of seven.
Reproduction prohibited without written consent of the author.
Your comments and suggestions are greatly appreciated:
e-mail: johnson@earthmatrix.com
Earth/matriX
Science in Ancient Artwork Nº.103
The Reciprocal of Seven and Pi in the Ancient
Reckoning System
11 April 1998
©1998-2012 Copyrighted by Charles William Johnson.
All Rights Reserved
Reproduction prohibited without written consent of the author.
| Home | Books | All Essays | Author |