A Multi-Gravitational Solar System, Infinitely so ...

Earth/matriX
SCIENCE IN ANCIENT ARTWORK
and SCIENCE TODAY

A Multi-Gravitational Solar System
Infinitely so...

By Charles William Johnson

Previously, I have been considering the solar system from the perspective of two center-points, that of the centerpoint of the Sun and the barycenter of the solar system as a centerpoint as well. In a sense, this bi-gravitational solar system is strictly for conceptual purposes only. For obviously one realizes that the solar system contains many planetary bodies (planets and their respective moons, plus the asteroids, the minor planets and the Sun itself). These varied relationships constitute a multi-gravitational solar system, which in fact is infinitely so once we consider the comets that fly in and around the system, plus the system as an essential part of the galaxy in which it resides.

Nonetheless, it is possible to isolate distinct relationships among the planetary bodies and consider them as of the proportions and ratios of their different characteristics and properties. In this essay, I will consider the multi-gravitational solar system, not the two main centerpoints alone, and present a distinct view of the relationships among the planetary bodies within our solar system. The reader will note that at times the values are slightly different for a particular datum from one essay to another; this occurs as distinct measurements are offered by the many different sources for these data in today's scientific literature. However, the general tendencies of the conclusions remain valid although values may vary by a few specific digits here and there.

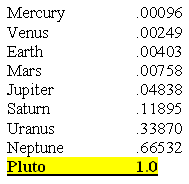
Generally, the planets are approached from the perspective of the planet Earth as acting like a baseline for all data concerning the other eight planets in the solar system. In this manner, the data referencing the Earth are generally assigned the value of unit 1.0. For example, the astronomical unit employed to measure distance in the Universe is often based on the astronomical unit (AU) representing the distance between the Sun and the Earth (roughly 93 million miles).

The Astronomical Unit (1.0)
Assigned to the Distance between the Sun the Earth

In a previous essay, I have suggested that the distance between the planet Mercury and the Sun (roughly 36 million miles) be used as an astronomical unit. The reasoning is simple. It appears to be to deficient to choose the third planet within the solar system from the Sun as a baseline measurement. It would be more acceptable, in my mind, to employ the outer or inner limit of the system to measure distance; i.e., respectively, the distance between the Sun and Pluto or, the distance between Mercury and the Sun. There appears to be little reason to choose the planet Earth as a baseline for measurement other than the fact that we live on this planet.

By employing the distance between the Sun and Mercury for the astronomical unit 1.0, a set of proportional numbers appear that resemble the set of numbers for the orbital times of the planets where Mercury's orbital period is employed as unit 1.0. First, let me, offer the numbers that were given in the earlier essay regarding the astronomical unit 1.0 for the mean distance between the Sun and Mercury, as may be seen in the following ratios:

The Distance of the Sun to the Planets: Mercury's Distance as Unit 1.0

The proportional progression of number is more visible when the astronomical unit of the distance between the Sun and Mercury is employed as shown above. The reader is invited to examine my essay on this theme posted on the web-site: www.earthmatrix.com.

Now, let me examine the orbital periods of the planets with other baselines of unit 1.0, besides that of the Earth. Again, to consider all of the planetary bodies in the solar system and their orbital periods as of the sidereal Earth year (365.256360 days) limits the perspective of a multi-gravitational solar system.

In order to better conceptualize the infinitely so gravitational relationships of the solar system in which we live, it is necessary to view the ratios among the planetary bodies from distinct perspectives. This means that we should not only consider the orbital times where the orbital year of Earth is considered unit 1.0, or even where the orbital time of Mercury is considered unit 1.0. In this case, it is best to consider all planets ar representing unit 1.0, alternately so.

The consideration of the orbital time of Mercury as unit 1.0 identifies ratios that I have not seen emphasized in the scientific literature. Also, make a comparison of the previously cited values for the distances of the planetary bodies to the Sun with the following data for the orbital periods of the planets where the orbital time of Mercury is assigned the unit value of 1.0. Consider the following:

The Orbital Time of the Planets with Mercury's Orbital Time as Unit 1.0

In this particular case, where the orbital time of Mercury is taken as baseline unit 1.0, the ratio of orbits between Mercury | Jupiter and between Mercury | Uranus are outstanding as whole numbers.

Now, consider a comparison of the values for distance and for orbital periods of the planets with Mercury's data as base unit 1.0. The ratio of 1.0 | 101.33 for distance and the ratio 1.0 | 1033.3 for orbital time portrays a system whereby these inner and outer limits serve as baselines, something that an assignment to the third planet in the solar system (Earth) does not portray.

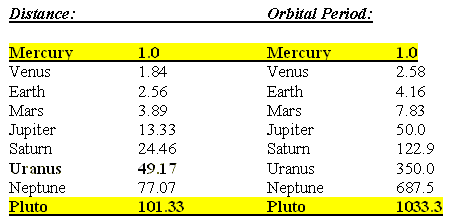
The mid-point for the distance terms falls upon Uranus (49.17), while the mid-point for the orbital time falls around midway between Uranus and Neptune (518.5).

Now, consider the assignment of unit 1.0 to the other planets in the solar system.

The Orbital Time of the Planets with Venus' Orbital Time as Unit 1.0

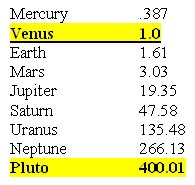
In the previous case, where the orbital time of Venus is considered to be the baseline unit 1.0, the ratio with Pluto is also outstanding as a whole number for the two mean distances.

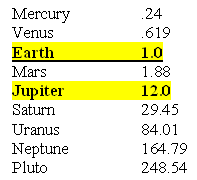
The Orbital Time of the Planets with Earth's Orbital Time as Unit 1.0

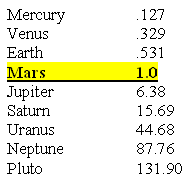
The Orbital Time of the Planets with Mars' Orbital Time as Unit 1.0

The Orbital Time of the Planets with Jupiter's Orbital Time as Unit 1.0

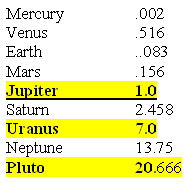
The Orbital Time of the Planets with Saturn's Orbital Time as Unit 1.0

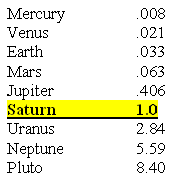
The Orbital Time of the Planets with Uranus' Orbital Time as Unit 1.0

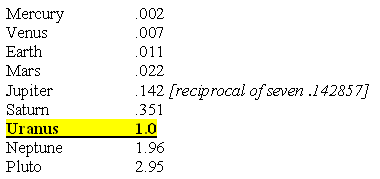
The Orbital Time of the Planets with Neptune's Orbital Time as Unit 1.0

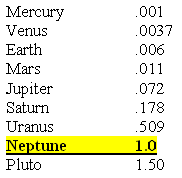
The Orbital Time of the Planets with Pluto's Orbital Time as Unit 1.0

Select Ratios Among the Orbital Times of the Planets

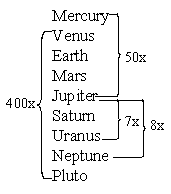
It is only logical that if the distance between the Sun and the planet Mercury may be considered to be astronomical unit 1.0, then the same conceptual procedure may apply to the orbital times of the planets, in as much as distance and time are intricately related in spacetime/movement. I can only see positive results from considering the orbital period of Mercury as a baseline unit 1.0 measurement for other astronomical periods.

One revolution of the solar system around the galaxy, the galactic cycle or the solar cycle, consists of 225,000,000 years.

225,000,000 x 365.256360 = 8.2182681 x10¹⁰ x 86400 seconds/day
equals
7.100583638 x10¹⁵ total number of seconds one solar cycle.

87.66144 days of Mercury orbital period x 86400 seconds
equals
7573948.416 seconds

Now, do the obvious, divide the number of seconds in one solar cycle by the number of seconds in one orbit of Mercury:

7.100583638 fractal / 7.573948.416 fractal = .937500924
1 / .937500924 = 1.06665615

Today, the barycenter of the solar system is shown to be between 1.066 and 1.068 solar radii. The same/similar proportion is to be found on distinct levels of the measurement of distance and of time within matter-energy in the Universe.