
The Solar System as Maya Long-Count
Charles William Johnson
The maya long count refers to various categories of day-counts
that have been identified as follows:
|
23,040,000,000
|
days
|
alautun
|
|
1,152,000,000
|
kinchiltun
|
|
|
57,600,000
|
calbatun
|
|
|
2,880,000
|
pictun
|
|
|
144,000
|
baktun
|
|
|
7,200
|
katun
|
|
|
360
|
tun
|
|
|
20
|
uinal
|
|
|
1
|
day
|
kin
|
In one of our first essays, we analyzed how there is a break between the category of twenty days and that of the 360c. In a sense, then, the range of 360c to 2304c (alautun) constitutes the main categories of the base and multiples of the tun, the 360c. Many scholars have identified the ancient 360c calendar as being in error, since they compare it to our present-day calendar. The tun has five days that added to it, in the same way as the ancient kemi 360c day-calendar existed. We have suggested repeatedly that these two ancients calendars were not in error, but possibly were more than calendars. In other words, the ancients may have been counting more than just the days with their reckoning systems.
We have suggested that the ancient reckoning systems may have been counting distances, for example, of the cosmos. Obviously, this is a rather daring thesis, since there is apparently no evidence in the historical record for such an affirmation. We have based our analyses solely upon the logic of numbers coming out of the ancient reckoning systems. And, we have suggested that even if the ancients were not counting distances, for example of the planets in our solar system, then, their ancient reckoning systems could well have accommodated such measurements.
In our recent studies of the solar system, once again, we find that the ancient reckoning system of the maya, the maya long-count, reflects an almost exact representation of the distances traveled by the planets. Let us look a little closer at just how exactly the system represents the solar system's composition.
In previous essays, we have called attention to the possibility of utilizing the Mercury/Sun distance as the astronomical unit (AU), instead of the commonly accepted Earth/Sun distance. The reasoning is obvious, since the Mercury/Sun average mean distance is 36,000,000 miles, while that of Earth/Sun is approximately 93,000,000 miles. One could say that this is cheating; we are accepting an obvious relationship to the maya long-count by choosing the Mercury/Sun distance, since it represents a fractal expression of the 360c day-count. Naturally, all of the distances expressed in the Mercury/Sun distance shall reflect a direct relationship between time and distance because of the sameness of the terms (36c).
But, one has to wonder whether the maya may have chosen the 360c day-count for their long-count precisely based upon this measurement. In other words, such a choice would have multiple meanings, one of which would be that the ancient reckoning system was far more complex than currently imagined by scholars. We have suggested that from the perspective of matter-energy, it is more logical to employ the Mercury/Sun relationship for the concept of astronomical unit (AU), than the Earth/Sun relationship.
In other words, it is more acceptable to employ one of the extreme relationships of the solar system (i.e., Mercury/Sun or Pluto/Sun) for a basic measurement of distance, than using one of the planets (i.e., Earth) within those two inner/outer boundaries. Obviously, scientists use Earth because we live on Earth; Earth is our most important planet as such, and we would like to know distances in terms of our own distance from the Sun.
But, from the perspective of matter-energy, and the laws that govern the make-up of solar systems, undoubtedly the inner/outer relationships of orbits are probably more significant. The relationships of Mercury/Sun and Pluto/Sun are the determining boundaries of our solar system, whereas Earth lies in between those natural boundaries.
Now, in terms of day-counts, the alautun (23,040,000,000 days) has always surprised scholars. Scholars feel that the ancients did not even count Earth's orbital timing properly, sicne the tun represents a 360c day-count, plus the additional five days tacked on at the end. It is difficult to think that a people who could not count a 365c day-count properly would evidently have trouble in counting an enormously long count such as the alautun category.
But, again, supposing the ancient maya were counting other aspects of nature, such as, the distance of the planets from the Sun or, the distance traveled by the planets around the Sun. Now, this is not an idea that is readily accepted, or even entertained by most scholars. It is a subject that is simply not on the syllabus of any classroom.
Nonetheless, once we begin to examine the contemporary numbers offered for the distances of the planets, then, it may well be that the ancient maya were counting not only the days, but the distance traveled by the planets.
The distance in miles from the Sun is generally measured in average mean distances, since the planets do not travel perfect circles, but elliptical orbits. However, one might suspect that the ancients, much like our own mathematicians and geometricians of today, think in ideal terms. The boundaries for the inner and outer planets of the solar system, then, are represented by Mercury (36,000,000 miles) and Pluto (3,667,000,000 miles) from the Sun.
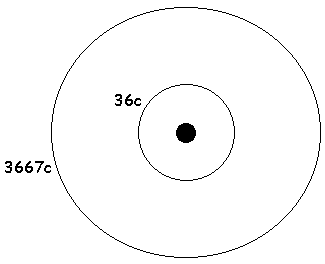
This particular circular design brings to mind many different pieces of ancient artwork, from the Aztec Calendar, to the representation of the Universe by the ancient Chinese. But, for now, the relationship defined by the inner and outer planets reflects an almost 1 : 100 scale.
3667 / 36 = 101.861111
Furthermore, one wonders whether the ancient 1001c might not even have had its origin in these numbers:
3 x 3667 = 11001
Such considerations must remain for another day, when we are more concerned with the inner workings of the numbers. For now, we are concerned with the geometry.
Without going into a discussion of the
different values for pi (![]() )
that have appeared in the historical record, let us simply work with the
value of pi as we know it today (3.141592654). If we were to consider
the numbers related to the circumference of a circle that uses the distance
of the planets from the Sun, i.e., as the radii of the formulae, then
the following would obtain. In other words, let us suppose that the ancient
also conceived of the circular orbits of the planets, and visualized the
corresponding numbers in terms of perfect circles or cycles.
)
that have appeared in the historical record, let us simply work with the
value of pi as we know it today (3.141592654). If we were to consider
the numbers related to the circumference of a circle that uses the distance
of the planets from the Sun, i.e., as the radii of the formulae, then
the following would obtain. In other words, let us suppose that the ancient
also conceived of the circular orbits of the planets, and visualized the
corresponding numbers in terms of perfect circles or cycles.
| 36c x 2 |
= | 226.1946711 | |
| 3667 x 2 |
= | 23040.44052 | [note fractal expression of alautun] |
In the previous numbers, we see that the distance of Pluto from the Sun as offered by today's figure, relates directly to the alautun number/fractal of the maya long count. If Pluto were to follow a perfect circle, then according to its distance from the Sun (in terms of the radii of that circle), then Pluto would have a circumference, or orbital distance, of a number that is close to the ancient maya long count category, the alautun (23,040,000,000).
| Just how close is this relationship. Let us add the zeros. | ||||
| 3,667,000,000 miles Pluto distance | ||||
| 3,667,000,000 x 2p = 23,040,440,520 miles | ||||
|
23,040,440,520
|
-
|
23,040,000,000 | = | 440,520 difference |
|
(miles/Pluto)
|
(alautun/maya) | |||
It would appear that the ideal, perfect circle traveled by Pluto nearly equals the same number of digits as that expressed by the maya long-count alautun. It is significant to note that the scholars have listed the alautun category as the last one on the commonly cited scale of the maya long count. as though it reflects the end of something, possibly the outer limit of our solar system. The solar system, then reflects the inner 36c of Mercury's distance from the Sun, and Pluto's 23040c for its ideal circumference.
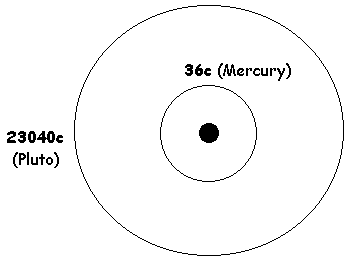
The maya long count begins with a significant 360c count (the tun), and ends with the alautun, 2304c count.
The solar system begins with the inner planet mercury, a 36c distance from the Sun, and ends its boundaries (as far as we know) with the 2304c count for the ideal circumference of the planet Pluto. There may be a planet beyond Pluto; such an idea has been suggested. But, possibly the extent of the knowledge expressed in the ancient maya system coincided with our own current knowledge of today, in only being able to recognize the outer boundary as being determined by Pluto's orbit
The maya are said to have worked with round numbers. Had they conceived of the ideal orbital path of Pluto as 23040000000, then the radius, or the mean average distance of Pluto from the Sun, would have to be 3666.929889 miles, a significant .070111 difference.
Adjustments may have been made. The maya are said to have had a precession count of 25956c years.
| 25956 / 360 | = | 72.1 | |
| 36.05 | x 2 |
One can only wonder whether the 2268c Nineveh count represented the distance of Mercury/Sun:
226.8 x 2![]() = 356.2566069
= 356.2566069
This figure is very significant in relation to the Earth's sidereal orbital time: 365.256 days.
365.256 - 356.256 = 9 [9, 18, 36, 72, 144, 288, 576, 1152, 2304]
Now, let us view the limits of the solar system in terms of ideal, circular orbits:
| [Distance million miles] | Ideal Circumference million miles] | ||
| Mercury | 36 x 2 |
= | 226.1946711 |
| Venus | 67.2 | = | 422.2300526 |
| Earth | 93 | = | 584.3362336 |
| 92.957 | = | 584.0660566 | |
| Mars | 141.5 | = | 889.070721 |
| Jupiter | 483.3 | = | 3036.663459 |
| Saturn | 886.1 | = | 5567.530501 |
| Uranus | 1783.0 | = | 11202.9194 |
| Neptune | 2793 | = | 17548.93656 |
| Pluto | 3667 | = | 23040.44052 |
If one were to consider the Mercury distance to be 225c, from the Venus sidereal count, then that would signify a mean average distance number of 353.4291735 (note, the ancient 354c day-count). Adjustments seem to be easily obtained in this manner. Further, one must note the fact that the Venus synodic orbital time (583.92) appears in the Earth's ideal circumference distance (584.33). The differences are minimal, and again, adjustments could easily be made. The ancients employed the 225c and the 584c counts for the sidereal and synodic cycles of Venus.
Even the average mean distances computed for the Asteroids (233.9 million miles) that lie between Mars and Jupiter reflects a similarly historical count.
233.9 x 2![]() = 1469.637043 [note the 1460c Sothic cycle]
= 1469.637043 [note the 1460c Sothic cycle]
Given the fact that the belt of the asteroids is so enormously wide, one could easily find the Sothic cycle figure in this range.
1460c / 2![]() = 229.3362637 [millions of miles]
= 229.3362637 [millions of miles]
One may wonder whether the ancients knew these events in the sky, whether they had computed the composition of the solar system. So many coincidences in the numbers cause one to suspect that they possessed this information. Consider the idea of the reciprocals of the boundaries of the system.
1 / 36c = .027777778
1 / 3667c = .0002727024816
Let us move the decimal place as a fractal expression in order to visualize the product better.
27.777778 x 27.27024816 = 757.5069 [note 756c of Great Pyramid]
| Adjustment: 756c / 27.77778 = 27.21599978 | [27.216] |
| 54432 | |
| 108864 |
The 108864c is an historically significant number found in the Meso-American record. One suspects that the measurement of the side of the Great Pyramid may have resulted from such computations with great ease. The 13.8888889c (half of the 27.777778c) is historically recognized in many forms:
| 365c / 360c | = | 1.013888889 | |
|
576 x 13.888889 |
= | 8000.000064 | |
| 432 x 13.888889 | = | 6000.000048 | |
| 18980c / 1.3888889 | = | 13665.5999 | [ 1366560c maya companion number; |
| 18980c days Meso-american calendar round] | |||
One must realize that the 1.3888889 number is simply the reciprocal of 72c, one of the most significant numbers in our universe and one of the most significant of the ancient reckoning system.
360c x 72c = 25920 [Platonic Cycle]
Observations
The solar system appears to follow the day-counts of the ancient reckoning system, or maybe one should state that inversely. The ancients appear to have recognized the composition of the solar system, and incorporated its numbers into their reckoning system. There are many ways to state the obvious; the ancients appear to have been scientifically plugged into reality.
They appear to have symbolized many of the events in the sky in their reckoning system. It may have been easier to simply show a system of 36 : 360; but by creating a system of 36 : 2304, somehow reflects an even more creative mind. In different ways, the solar system is both of these systems, as we have examined in this extract. To find a number that is also equal, if not exactly the same, to the maya alautun (23040000000) in the ideal circumference of the outer limit of the solar system somehow defies the very concept of coincidence. Yet, that very relationship exists. There does not appear to be any concept of happenstance, but rather one of conscious design.
The question appears to be just how far does the concept of design go. It is easy to comprehend an ancient reckoning system reflecting the design of the solar system, and symbolizing its elements. The problem arises when one begins to question the concept of design in matter-energy itself. In other words, the solar system itself appears to reflect a conscious design of its own. That is an even more intriguing thought for further analysis.
*****
2000-2013 Copyrighted by Charles William Johnson. All rights reserved. Reproduction prohibited.
The Solar System as Maya Long-Count
Extract 68
3 October 2000
Earth/matriX:
Science in Ancient Artwork,
P.O. Box 231126, New Orleans, LA 70183-1126.
| Home | Books | Author |