Science in Ancient Artwork
THE MAYA-KEMI BASELINE: 1-6-8-9
by
Charles William Johnson
The significance of the 3-4-5 right triangle has often been cited within the designs of ancient artwork. The numbers of the 3-4-5 right triangle gave way to the Pythagorean Theorem at a much later date in history. In our studies, we have perceived a relationship of a series of 3-4-5 right triangles as of the extension of the Pythagorean Theorem, which we have already analyzed in previous essays and extracts:
| Pythagorean Theorem | Extension of the Pythagorean Theorem | |
| x² + y² = z² | x³ + y³ + z³ = x'³ |
The extension involves the cube of the terms of the Pythagorean Theorem, whereby the x-prime term indicates the following dimension of the next right triangle on the series. (Cfr., Earth/matriX Nº57). This particular relation of equivalency appears to have significance for Fermat's Last Theorem as well, which has been expressed as x³ + y³ = z³ an idea which to date has not been illustrated fully in numbers. As we have shown already, if the sum of two terms to the cube could equal a third term to the cube, then the extension might be incorrect. However, the case is rather the opposite; Fermat was correct; his last theorem is impossible to attain in numbers, whole numbers that is.
In order to better comprehend the Pythagorean Theorem and Fermat's Last Theorem, one might consider what appears to have been another relationship that the ancient mathematicians had identified and used in their computations and designs, but which has undoubtedly been lost until now. One must search for another relationship of equivalency of terms before the 3-4-5 relation which serves as the basis of the Pythagorean Theorem itself. This relation may be found in the numbers 1-6-8-9 to the cube; once again, we shall employ the extension formula, although we now realize that these numbers do not reflect a right triangle, or any triangle for that matter.
| x³ + y³ + z³ = x'³ | may be | 1³ + 6³ + 8³ | = | 9³ |
| 1 + 216 + 512 | = | 729 | ||
| 729 | = | 729 |
It is understandable that three lines of a measurement of 1-6-8 would not even form a triangle, but rather one could imagine a figure that is well known throughout much of ancient artwork, especially among the maya:
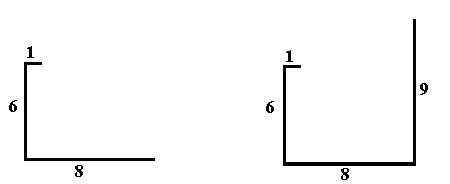
From this particular relation of equivalency, an infinite series of equivalencies may be established as occurs with the extension of right triangles; only now the figure would be that L-shaped figure as shown above.
| 1 | - | 6 | - | 8 | - | 9 | ||||||||
| 2 | 12 | 16 | 18 | |||||||||||
| 3 | 18 | 24 | 27 | |||||||||||
| 4 | 24 | 32 | 36 | |||||||||||
| 5 | 30 | 40 | 45 | i.e., |
5³
|
+ |
30³
|
+ |
40³
|
= | 45³ | |||
| ... | ... | ... | ... |
125
|
+ |
27000
|
+ |
64000
|
= | 91125 | ||||
|
91125
|
= | 91125 |
Any numbes of imaginable geometric design may be conceived as of this L-shaped baseline, as of a series of progressively larger Ls, or as of an L that circles back upon itself; etc.
 |
|
Strikingly, one might even consider a design as of the pyramid similar to that employed in ancient Egypt (kemi) whose angle of inclination could be precisely 52º.
 |
5.5 / 7 = .785714286
962 x .785714286 = 755.8571479 (The east wall of the Great Pyramid has been measured at 755.88 feet; 962 being double the 481 ft. projected height thereof.) |
A strong case may be made to show how the 1-6-8-9 baseline, presented as an L-shaped figure may have been translated into the geometry of ancient artwork. In later analyses we ahall treat this particular theme in greater detail. For now, our concern regards the mathematical aspects of the baseline numbers. The extension numbers (3-4-5-6) and the baseline numbers (1-6-8-9) when multiplied by the natural numbers offer the following results:
| 3-4-5-6 | x | 1 | = | 6 | 1-6-8-9 | x | 1 | = | 09 | |
| 6 | x | 2 | = | 12 | 9 | x | 2 | = | 18 | |
| 6 | x | 3 | = | 18 | 9 | x | 3 | = | 27 | |
| 6 | x | 4 | = | 24 | 9 | x | 4 | = | 36 | |
| 6 | x | 5 | = | 30 | 9 | x | 5 | = | 45 | |
| 6 | x | 6 | = | 36 | 9 | x | 6 | = | 54 | |
| 6 | x | 7 | = | 42 | 9 | x | 7 | = | 63 | |
| 6 | x | 8 | = | 48 | 9 | x | 8 | = | 41 | |
| 6 | x | 9 | = | 54 | 9 | x | 9 | = | 81 | |
| 6 | x | 10 | = | 60 | 9 | x | 10 | = | 90 | |
| ... | ... | ... | ... | ... | ... |
In these two cases, the fourth term of the 4-term equations is either a 6 or a 9, and multiples thereof ad infinitum. In order to find the terms of an equation whose forth-term would be a 3, one would simply select the 5 x (3-4-5-6)set:
| 15 - 20 - 25 - 30 | ||
| 15³ + 20³ + 25³ = 30³ | (27000 = 27000) |
Whereby the term 30, could be considered as a fractal-3 numbers; as all numbers of multiple of three. These three equations (15-20-25-30; 3-4-5-6; 1-6-8-9) would be illustrating that all numbers that are multiples of 3, 6 and 9 ad infinitum when set to the cube would have relations of equivalency to the corresponding three cubed terms of the same multiple number. All other numbers (1, 2, 4, 5, 7, 8) when employed as the fourth term of any one of these equations, and their multiples ad infinitum thereof, would have fractional expressions in one of more of the other terms correspondingly therof. Only those equations ending with a 3, 6, or 9 (and their multiples) will produce relations of equivalency in whole numbers (without fractions) of their terms.
These relationship have a relevance for Fermat's posited theorem.
An ancient mathematician who surely knew that
3³ + 4³ + 5³ = 6³
inmediately knew that x³ + y³ = z³ was incorrect; say, where 6³
might be equal to any of the other two terms; as far as whole
numbers go, 6³ can only be equal to 3³+ 4³ + 5³; any other
proposition would obviously be in error. Had Fermat known the
nature of the equivalency of terms of the natural numbers as of
the extension of the Pythagorean Theorem to the cube, then he
would not have considered the possibility of his cited last
theorem. Gauss must have suspected all of this when he ignored
Fermat's challenge.
Let us offer a single example to illustrate the previous point based on the concept of fractals:
| 17 x | 15-20-25-30 | ||
| 255³ + 340³+ 425³ = 510³ | or as a fractal | 25.5³ + 34.0³ + 42.5³ = 51.0³ |
Both relations are equivalencias; only the first (510³) is expressed entirely in whole numbers. By moving the decimal one place to the left (as fractals), the 51.0³ is no longer a multiple of 3 (510 / 3 = 170), and therefore its resolution will produce fractions. Therefore, in order to fulfill Fermat's request that all numbers be expressed in whole numbers (no fractions) one would have to employ an equation of four terms to the cube, whereby the numbers or term z to the cube would have to be a multiple of 3, 6, or 9.
The equation of the baseline is quite unique, and reflects significant numbers. Let us consider when the fourth term of the equation might be one (1), as may be visualized as follows:
| 1 | 6 | 8 | 9 | / 3 | ||||
| .333333333 | 2 | 2 | .666666666 | 3 | / 3 | |||
| .111111111 | .666666666 | .888888888 | 1 | / 3 | ||||
| .037037037 | .222222222 | .296296296 | .333333333 | / 3 | ||||
| .012345679 | .074074074 | .0987654321 | .111111111 | / 3 |
A significant procedure within the ancient reckoning system is that of doubling/halving numbers; but also it would appear that multiplying and dividing by 3 is also significant. We have also seen how this last row of numbers may have been registered in the numbers of the Legend of the Four Suns (Cfr., Earth/matriX Nº15):
| 100 / 81 | = | 1.234567901 |
| 8 / 81 | = | .0987654321 |
The 1:8 relation of the 1-6-8-9 set baseline concerns the same count: 64c, coming out of the natural progression.
|
1, 2, 4, 8, 16, 32,
64...
|
| 8, 16, 32, 64... |
That is for the 2x progression; by multiplying by 3x, the progressions would be a 27c for the 1, and a 24c for the 8 of the 1-6-8-9 baseline numbers:
| (3x) | 1, 3, 9, 27... | (3x) | 8, 24... |
Now consider the relevancy of the maya numbers as of the 1-6-8-9 baseline. We shall use the 1, 2, 4, 16, 32, 64... progression for the first term of the equation:
The baseline numbers:
| 1 | 6 | 8 | 9 | 3 | 4 | 5 | 6 | |
| 2 | 12 | 16 | 18 | 9 | 12 | 15 | 18 | |
| 4 | 24 | 32 | 36 | 18 | 24 | 30 | 36 | |
| 8 | 48 | 64 | 72 | 36 | 48 | 60 | 72 | |
| 16 | 96 | 128 | 144 | 72 | 96 | 120 | 144 | |
| 32 | 196 | 256 | 288 | 144 | 192 | 240 | 288 | |
| 64 | 384 | 512 | 576 | 288 | 384 | 480 | 576 | |
| 128 | 768 | 1024 | 1152 | 576 | 768 | 960 | 1152 | |
| 256 | 1536 | 2048 | 2304 | 1152 | 1536 | 1920 | 2304 | |
| 512 | 3072 | 4096 | 4608 | 2304 | 3072 | 3840 | 4608 | |
| ... | ... | ... | ... | ... | ... | ... | ... | |
| Remember these numbers of the extension of the Pythagorean Theorem to the cube for the maya numbers also. (Cfr. Earth/matriX Extract Nº1) | ||||||||
The cube of the maya numbers (fractals) may be equivalent to the sums of the cube of the terms of the numbers (fractals) which accompany each one on the previous chart. As may be observed the numbers are whole numbers. In order to get a feel for the numbers, one may observe how some of the sum of the terms offter other possibilities for exponential expressions of the maya numbers. For example, some of the sum of the terms to the cube offer maya numbers which have square roots; others do not;
|
or, |
|
|
or, |
|
Some maya numbers/fractals have even-numbered square roots; some do not, for some are fractions. Again, the maya may have understood that Fermat's Last Theorem (x³ + y³ = z³) was not a possibility for the maya numbers, since they already knew that it was more a case for some of their numbers that x³ + y³ = z²
One simple answer to Fermat's conjecture, then, could simply be that x³ + y³ does not equal z³, for many (infinite) whole numbers, because the sum of those two terms equals rather z² (z-square; not z-cube).
The greater concern lies with the maya-kemi numbers themselves (respectively, 576 and 756) rather than with the posits of Fermat. The need arises regarding how to visualize the maya numbers in terms of the artwork; for example, consider the relevant expressions above of
| 64 | - | 384 | - | 512 | - | 576 | and | 576 | - | 768 | - | 960 | - | 1152 |
| (The baseline numbers) | (The extension numbers) | |||||||||||||
whereby 576 ends and begins a relation; or, as relations of equivalency as options:
| 64 | - | 384 | - | 512 | - | 576 | and | 288 | - | 384 | - | 480 | - | 576 |
The ancient artwork is proportionally relational; the concept of progression may be seen in the math (as doubling/halving numbers), and in the geometrical patterns that repeat themselves in an incremental and diminshing fractal order. The baseline numbers of the 1-6-8-9 set and their multiples thereof, alongwith the extension numbers of the 3-4-5-6 set and their multiples thereof, both contain possibilities that reflect the maya and the kemi numbers of both ancient reckoning systems. Any suggestion that all of these relationship are due to mere coincidence of terms, somehow rings hollow to this author. Time and again, throughout the Earth/matriX studies, we have seen how the coincidence of numbers allows for mathematical computations that duplicate some of the knowledge we have about the ancient maya and the ancient kemi. One suspects that such coincidences were seen by the ancient artists who may surely have incorporated these numbers into their designs. Symbolically, even the square roots of the chosen maya companion number, 1366560, reflects the terms of the 1-6-8-9 numbers:
In subsequent essays, we shall attempt to comprehend how these numbers may be read within the ancient time-reckoning system itself.
Your comments and suggestions are greatly appreciated:
e-mail: johnson@earthmatrix.com
Science in Ancient Artwork
Extract Nº.6
The Maya-Kemi Baseline:1-6-8-9
26 December 1996
©1996-2015 Copyrighted by Charles William Johnson. All Rights Reserved
Earth/matriX,
Reproduction prohibited without written consent of the author.
| Home | Releases | Forum | Reviews | Links | Author |