
The Sound of Meaning: Comparative Linguistics
of Ancient Egyptian,
Maya and Nahuatl
154 pages
ISBN 0.9755482-04
Purchase in Amazon
Price: $3.99 US

Purchase in Amazon
this Earth/matriX eBook
The Goldbach Conjecture
and the Universe
of Primes
182 pages
Price $7.99

Purchase in Amazon
this Earth/matriX eBook
Particle Mass Diference
Price $7.99 US
212pags

Extract No.26
Ancient
Pi (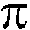 ):
):
Knowers of the Universe
By
Charles William Johnson
Any practical attempt to divide the diameter of a circle
into its own circumference can only meet with failure. Such a procedure
is entirely theoretical in nature. Dividing unlikes, a straight line (the
diameter of a circle) into a curved line (the circumference of a circle)
can only be met with frustration. The kind of frustration that is portrayed
throughout history in humankind's attempt to measure the incommensurable.
No matter how hard one may try, even with the assistance of contemporary
electronic computers, bending either the straight line or the curved line,
alters the nature of the problem and yields an impossibility. As soon
as one of the lines is bent the results are tainted. Then, there is the
question of the very thickness of the lines being measured in length.
Whether one measures the inner part of the curved line of the circumference
or the outer edge makes a great deal of difference; especially, when one
is attempting to achieve an exactness in the concept of pi ( ![]() ) to hundreds or even thousands of decimal places.
) to hundreds or even thousands of decimal places.
If we realize that the measurement of the ratio between the diameter and
the circumference of a circle is entirely theoretical and speculative,
then we may also realize that the result shall always represent an approximation.
In fact, the very fact that pi is always expressed in terms of an unending
fraction (with mathematicians searching it to the nth number of
decimal places), should cause us to accept the idea that pi can only be
an approximation. (As Lambert illustrated in 1767, " ![]() is not a rational number, i.e., it cannot be expressed as a ratio of two
integers"; Beckmann, p.100.)
is not a rational number, i.e., it cannot be expressed as a ratio of two
integers"; Beckmann, p.100.)
Once we realize that pi represents a fractional expression in numbers,
it were as though either nature itself were wrong, or the numbers must
surely be able to be manipulated to render whole numbers. The ancients
sought to work with whole numbers. However, once we realize that the ancient
reckoning system may have been based upon the concept of a floating decimal
place, then we should understand that all numbers, in fact, may be visualized
as whole numbers. The cut-off point becomes one of arbitrary choice at
times. With regard to the concept of pi, contemporary mathematicians have
not decided to accept that arbitrary cut-off point, and continue to search
for the unending decimal expression of pi. At one time, not too long ago,
pi was simply represented to be 3.1416; and, in a practical sense, it
served all purposes of constructing things out of matter and energy. Today,
the unending expression of pi to hundreds of thousands of decimal places
serves no practical purpose that we know of, at least, other than that
of an unending contest to discover the ultimate expression of pi. One
has only to admire the relation of the diameter of any circle to its circumference
to note that particular expression.
Throughout history, the expression of pi has taken on many variations. Petr Beckmann (Cfr., A History of ![]() (pi), Golem, 1971), offers an exemplary analysis of the concept
throughout history. The Babylonians 3 1/8;
the Egyptians 4(8/9)²; Siddhantas,
3.1416; Brahmagupta, 3.162277; Chinese, 3.1724; Liu Hui,
3.141024 <
(pi), Golem, 1971), offers an exemplary analysis of the concept
throughout history. The Babylonians 3 1/8;
the Egyptians 4(8/9)²; Siddhantas,
3.1416; Brahmagupta, 3.162277; Chinese, 3.1724; Liu Hui,
3.141024 < ![]() < 3.142704; Liu Hui, 3.14159; Tsu Chung-Chih, 3.1415926
<
< 3.142704; Liu Hui, 3.14159; Tsu Chung-Chih, 3.1415926
< ![]() < 3.1415927; Archimedes, 3.14084 <
< 3.1415927; Archimedes, 3.14084 < ![]() < 3.142858 (31/7); Heron, 3.1738; Ptolemy,
3.14167; Fibonacci,
< 3.142858 (31/7); Heron, 3.1738; Ptolemy,
3.14167; Fibonacci, ![]() = 864:275 = 3.141818; Viète, 3.141592635 <
= 864:275 = 3.141818; Viète, 3.141592635 < ![]() < 3.1415926537; and, finally in the computer language of FORTAN: 3.14159265358979324.
Again, citing Beckmann (p.101): "There is no practical or scientific
value in knowing more than the 17 decimal places used in the foregoing,
already somewhat artificial, application".
< 3.1415926537; and, finally in the computer language of FORTAN: 3.14159265358979324.
Again, citing Beckmann (p.101): "There is no practical or scientific
value in knowing more than the 17 decimal places used in the foregoing,
already somewhat artificial, application".
Nonetheless, in 1844, Johann Martin Zacharias Dase calculated ![]() to 200 decimal places, with the first zero appearing at the 32nd decimal
place ---meaning, possibly that the exercise should have ended there.
It has not; just as pi is an unending fraction, so is the human practice
of finding the number of unending decimal places in pi.
to 200 decimal places, with the first zero appearing at the 32nd decimal
place ---meaning, possibly that the exercise should have ended there.
It has not; just as pi is an unending fraction, so is the human practice
of finding the number of unending decimal places in pi.
Decimal hunting games aside, the practical uses of knowing pi (the ratio
of the diameter of a circle to its circumference) even as an approximation
has infinite applications in astronomy. And, the ancients were on the
whole astronomers; knowers of the universe. This ratio becomes
significant in calculating the movements of the planets and the stars;
in computing their coming and going in the sky. Once more, since we are
dealing with movement, the movement of the planetary bodies and the stars,
we are always speaking about approximations; even in and especially so
in astronomy. Therefore, the approximations to pi serve a purpose in knowing
the approximate movements of the planets. Such are the problems concerning
the measurement of moving bodies. As soon as they have been measured,
they have already moved from that measurement.
When we observe the measurements offered by Tsu Chung-Chih given
above, it becomes obvious that ancient approximations were at times far
ahead of latter day computations. And, then there is the problem that
one may obtain pi to the nth decimal place, but such decimal expressions
are beyond the human capacity to measure or even observe matter-energy
to such a minute degree.
In our analyses, we cannot cite any specific ancient documents for the
computation of pi among the ancients. Yet, the historically significant
numbers that do exist within the ancient reckoning systems may reveal
some partial aspects of the computations themselves. No matter which contemporary
studies we examine, pi is always given in relation to the number ca. 3.1-something,
as a guidepost. Yet, it may be the case that the ancients conceived of
pi in relation to the number of divisions that made up the circle; the
number of degrees or segments contained therein.
The concept of pi refers to the constant ratio of the diameter:circumference
of any circle; irrespective of the number of degrees contained within
that circle. Historically, the Babylonians came to use the number 360
for the divisional segments within a circle, and we have employed that
same number ever since. The abstracted universal circle, then, would have
a constant diameter of one (1.0), and the length of its circumference
would be pi ( ![]() ) of that: 3.1-something (whichever one might choose). Hence, diameter
is 1.0 in length; while, circumference is 3.141592654 (for example) in
length.
) of that: 3.1-something (whichever one might choose). Hence, diameter
is 1.0 in length; while, circumference is 3.141592654 (for example) in
length.
Now, if we consider the circumference to be divided into 360 degrees
(or segments; angular divisions with lines cutting through the center
of the circle as we know them), then using the contemporary figure for
pi (3.141592654), the length of the circumference could be 360 units,
while the length of the diameter would be 114.591559 (i.e., 360
/![]() ).
).
Now, let us suppose that the circle is divided into 260 degrees
(something that we are unaccustomed to considering, in fact). If we employ
the same length of the diameter of the previous example (114.591559),
then the relational figure for pi for a 260-degree circle would be: 2.268928028.
With that something very intriguing developes. Within ancient Nineveh,
there exists an historically significant fractal number cited as 2268.
One could imagine that the 2268 fractal number may relate to the concept
of proportion (i.e., pi) regarding a 260-division circle. The number 260
is relevant because during ancient times there existed in various cultures
a calendar based on a 260c day-count. Furthermore, the Great Cycle of
the sun, known as Precession, also involves a fractal of 260 (i.e., 26000
years). Now, were we to consider the Nineveh number for representing pi
on a 260-degree circle, then the constant value for the diameter would
then be 114.638448 (i.e., 260 / 2.268).
The use of the reciprocal of seven number (114.284714) for the length
of the 360 and 260 circle would offer the following values for pi, respectively:
| 360 / 114.285714 | = | 3.150000008 | (pi proportion for 360c circle) |
| 260 / 114.285714 | = | 2.275000006 | (pi proportion for 260c circle) |
Note that the 3.15 number offers a mediatio/duplatio series
based on the 63c, which was significant in ancient reckoning systems:
315, 630, 1260, 2520, 5040, 10080, 20160, 40320, 80640, 161280, 322560,
645120,1290240, 2580480 (a Precession number/fractal); and, 63,
126, 189, 252, 315, 378, 441, 504, 567 (kemi), 630, 693 (Sothic), 756 (Giza), 819 (k'awil; maya), 882, 945, 1008,
1071, 1134 (Nineveh, 2 x 1134 = 2268), 1197, etc.
Note that the 2275 fractal number is relevant for the computational
series within the ancient reckoning system of the 364c day-count:
2275, 4550, 9100, 18200, 36400, etc. Also, note that the difference
between the Nineveh 2268c and the pi-like number 2275 is seven (2275 -
2268 = 7); which could be easily translated from one series to the other
by remainder math based on multiples of seven.
Many of the distinctive historically significant numbers of the ancient
reckoning system reflect a relationship based on the reciprocal of seven.
Consider the maya long count period number of 1872000, which
has received so much speculation regarding its beginning and ending date.
Also, consider the period called the k'awil of the maya cited as
consisting of 819c days. Now, notice the number that obtains from
the division resulting from half of the long count period figure by the
k'awil: 936 / 819 = 1.142857143. The same figure obtains
regarding the constant length of a diameter of a circle based on a pi-like
number in relation to the reciprocal of seven as explained earlier.
Other relationships obtain regarding similar historically significant
numbers from other systems. The Great Pyramid entails the number 756c
as its baseline. Also, there exists the 432c number/fractal associated
with the Consecration. If we double the 432 figure and divide by the 756c,
the same result obtains: 864 / 756 = 1.142857143. Consider: 360
x .864 = 311.04 (31104 being an historically significant number for China
and Mesoamerica).
The significance of seven and its reciprocal becomes obvious throughout
the historically significant numbers/fractals. Even the obvious relationship,
of the 364c day-count of ancient Mesoamerica, which was employed for computations,
reveals a direct basis of seven: 364 / 7 = 52. Immediately, one
will recognize the 52c that is so well-known in ancient Mesoamerica as
the calendar round (52 years times 365 days = 18980 days; and 52 years
times 360 days = 18720! days). And, the ancient kemi appear to have employed
a 54c in its place: 7 times 54 = 378 (2 x 378 = 756; or, 7 x 108
= 756). No matter where one turns, the number seven and its reciprocal
make their appearance. The reasoning behind this procedure may be rather
obvious, although we have not discerned it previously.
The number 1.142857143 concerns the ratio 8/7ths. The Aztec Calendar appears
to be based upon a spatial division that reflects the logic of 7:8 or
8:7, depending upon the rings and segments to be considered (Cfr., Earth/matriX
No.88). If one were attempting to consider the diameter of the Solar
System, or the Universe, knowing that these events consist of imaginary
circles (ellipses), then the use of the unit 1.0 for the length of their
respective diameters would not be of much value. And, furthermore, if
the ancients had employed the contemporary (and possibly past) concept
of pi (based on a close approximation to 3.141592654, give or take a fraction),
then the numbers would have been unmanageable and not very attractive.
The apparent relational aspects of the many different historical numbers
found in the many distinctive ancient reckoning systems suggest a common
origin and reasoning. If the length of the diameter of the solar system
or the Universe were assigned a value consisting of the reciprocal of
seven (i.e., 1.142857143), then this would be the next best thing to working
with whole numbers for computing the time cycles of the movement of the
planetary bodies and the stars. Furthermore, knowing the actual measurement
of pi (the exact proportion of the diameter:circumference ratio) could
be compensated with remainder math adjustments quite easily. Consider
the following computations:
| 1.142857 | x | 819 | = | 935.999883 | (936) | (maya long count fractal) |
| 1.285714 | x | 819 | = | 1052.999766 | (1053) | |
| 1.428571 | x | 819 | = | 1169.999649 | (1170) | (Venus sidereal count) |
| 1.571428 | x | 819 | = | 1286.999532 | (1287) | |
| 1.714285 | x | 819 | = | 1403.999415 | (1404) | (kemi count; 351c) |
| 1.857142 | x | 819 | = | 1520.000298 | (1521) | (39²) |
| 1.142857 | x | 315 | = | 359.999955 | (360) | (360c; kemi; maya) |
| 1.285714 | x | 315 | = | 404.99991 | (405) | (1296000c; kemi) |
| 1.428571 | x | 315 | = | 449.999865 | (450) | (maya long count; 9 base system) |
| 1.571428 | x | 315 | = | 494.99982 | (495) | (99c lunar count) |
| 1.714285 | x | 315 | = | 539.999775 | (540) | (kemi count) |
| 1.857142 | x | 315 | = | 584.99973 | (585) | (Venus synodic count) |
One of the most interesting realtionships of this nature concerns the
2268c Nineveh count:
| 1.142857 | x | 2268 | = | 2591.999676 | (2592) | (Platonic Year, 25920 years) |
Scholars consider the figure of 3 1/7ths to
have been an erroneous computation for pi. Yet, we have never really known
how the ancients computed their mathematics. The few documents that remain
(such as the Rhind document of the ancient kemi) concern everyday matters;
not the mathematics and geometry of the study of the Universe. By employing
the reciprocal of seven in the computations, which is what an initial
analysis of the historically significant numbers reveals, the ancients
may have been seeking an easier method for arriving at their knowledge
of the Universe than what is offered by the precise unending fractional
expression of pi, the proportion of the diameter to the circumference
of a circle. This may be further understood when we realize that the comings
and goings of the planetary bodies and the stars throughout the Universe
do not travel on perfect pi-like circles.
The ancients may have employed distinct constant fractals/numbers for
adjustments in their computations: the length of the diameter may
have been based on 114.2857, 114.591559, 114.638448; etc; the distance
of the circumference may have been related to the 260c, 360c, 378c,
936c, etc.; and, the pi ratio (proportion) of the diameter:circumference may have been 2.268, 3.15, 3.1416, 3.142857, 819, etc. The distinctive
historically significant numbers reflect different aspects of the computations
and their corresponding adjustments. From this dynamic perspective, the
historically significant numbers may be communicating to us a much more
precise knowledge of astronomy and mathematical and geometrical computations
than we have been willing to concede to the ancients.
e-mail: Charles W. Johnson
©1998-2013 Copyrighted by Charles William Johnson. All rights reserved.
*************************
Links:
Ancient Phi and Its Extension
The Concept of Pi and the Ancient
Reckoning Numbers (Trigono/metriX)
| Home | Books | Author | All Essays |
